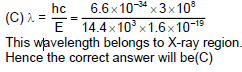Electromagnetic Waves

DISPLACEMENT CURRENT

(i) Circuit with Capacitor

Let us consider a circuit containing the capacitor as shown in fig. 21.1

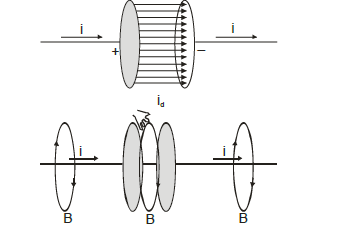
Circuit Diagram: A capacitor connected in a circuit with current flowing through connecting wires but not through the space between plates

(ii) Ampere's Circuital Law

According to Ampere's circuital law, the line integral of magnetic field along any closed path is μ₀ times the total current enclosed by the closed path. Mathematically:

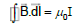
In this law it is assumed that conduction current flows through the connecting wires charging the condenser plates but no current flows in the space in between the plates. Actually it is not true.

Illustration 1: In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency 2 × 10¹⁰ Hz and amplitude 48 V/m. The amplitude of oscillating magnetic field will be:

Options:

(A) 1.6 × 10⁻⁸ Wb/m²

(B) 16 × 10⁻⁸ Wb/m²

(C) 12 × 10⁻⁷ Wb/m²

(D) 1.2 × 10⁻⁷ Wb/m²

Solution:

(B) Oscillating magnetic field

B = E/c = 48/(3 × 10⁸) = 16 × 10⁻⁸ Wb/m²

(iii) Maxwell's Modification

When the circuit is closed, conduction current flows from the plate P of the capacitor to the other plate Q through the conducting wires. Maxwell suggested that due to time varying electric field between the plates, an electric current, called displacement current (I_D), also flows across the space between the plates of the capacitor.

(iv) Continuous Current Flow

Thus, there is a continuous flow of current in a capacitive circuit also, through the conducting wire there is flow of conduction current I_C and through the space across the plates of capacitor, there is flow of displacement current I_D.

(v) Ampere-Maxwell's Circuital Law

Maxwell pointed out that in Ampere's circuital law, the current I should be treated as total current i.e., the sum of the conduction current I_C and displacement current I_D and modified the law as:

∮ B⃗ · dl⃗ = μ₀(I_C + I_D)

It is called the Ampere-Maxwell's circuital law.

(vi) Displacement Current Definition

The displacement current is defined as:

I_D = ε₀ (dΦ_E/dt)

where Φ_E is the electric flux linked between the plates of the capacitor at any instant.

Therefore Ampere-Maxwell circuital law may be expressed as:

∮ B⃗ · dl⃗ = μ₀[I_C + ε₀(dΦ_E/dt)]

Illustration 2: A parallel plate capacitor of plate separation 2 mm is connected in an electric circuit having source voltage 400V. If the plate area is 60 cm², then the value of displacement current for 10⁻⁶ sec. will be:

Options:

(A) 1.062A

(B) 1.062 × 10⁻²A

(C) 1.062 × 10⁻³A

(D) 1.062 × 10⁻⁴A

Solution:

(D) I_D = ε₀(dΦ_E/dt) = ε₀(d(EA)/dt) = ε₀A(dE/dt) = ε₀A(V/d)/t

I_D = (8.85 × 10⁻¹² × 400 × 60 × 10⁻⁴)/(2 × 10⁻³ × 10⁻⁶) = 1.062 × 10^-4A

Illustration 3: In an electric circuit, there is a capacitor of reactance 100Ω connected across the source of 220V. The displacement current will be:

Options:

(A) 2.2A

(B) 0.22A

(C) 4.2A

(D) 2.4A

Solution:

(A) Displacement current and conduction current are equal.

I_D = E/Z = 220/100 = 2.2A

(vii) & (viii) Important Properties

• The conduction current and the displacement current are always equal, i.e., I_C = I_D
• Like conduction current, the displacement current is also the source of magnetic field

Also Read: Electrostatic Potential and Capacitance

MAXWELL'S EQUATIONS AND LORENTZ FORCE

The existence of electro-magnetic waves that propagate through the space in the form of varying electric and magnetic fields has been predicted by the four basic laws of electromagnetism which are called Maxwell's equations.

(i) Maxwell's First Equation - Gauss's Law in Electrostatics

It states that the total electric flux through any closed surface is equal to 1/ε₀ times the net charge enclosed by

Mathematically,

∮ E⃗ · ds⃗ = q/ε₀

This equation is called Maxwell's first equation.

(ii) Maxwell's Second Equation - Gauss's Law in Magnetism

It states that the net magnetic flux crossing any closed surface is always zero.

Mathematically,

∮ B⃗ · ds⃗ = 0

This equation is called Maxwell's second equation. A direct consequence of this equation is that the magnetic monopoles do not exist.

(iii) Maxwell's Third Equation - Faraday's Law of Electromagnetic Induction

It states that the induced emf produced in a circuit is numerically equal to the rate of change of magnetic flux through it.

Mathematically,

ε = -dΦ_B/dt

But ε = ∮ E⃗ · dl⃗ = Line integral of electric field.

∮ E⃗ · dl⃗ = -dΦ_B/dt

This equation is called Maxwell's third equation.

The negative sign in this equation indicates that the induced emf produced opposes the rate of change of magnetic flux.

Illustration 4: A point source of electromagnetic radiation has an average power output of 800W. The maximum value of electric field at a distance 3.5m from the source will be:

Options:

(A) 56.7 V/m

(B) 62.6 V/m

(C) 39.3 V/m

(D) 47.5 V/m

Solution:

(B) Intensity of electromagnetic wave given is by

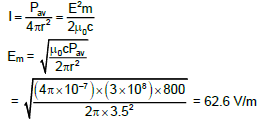
Illustration 5: In the above problem, the maximum value of magnetic field will be:

Options:

(A) 2.09 × 10⁻⁵ T

(B) 2.09 × 10⁻⁶ T

(C) 2.09 × 10⁻⁷ T

(D) 2.09 × 10⁻⁷ T

Solution:

(C) The maximum value of magnetic field is given by

B_m = E_m/c = 62.6/(3 × 10⁸) = 2.09 × 10⁻⁷ T

(iv) Maxwell's Fourth Equation - Maxwell-Ampere Circuital Law

It states that the line integral of magnetic field along a closed path is equal to μ₀ times the total current (i.e., sum of conduction and displacement currents threading the surface bounded by that closed path)

Mathematically,

∮ B⃗ · dl⃗ = μ₀[I_C + ε₀(dΦ_E/dt)]

This equation is called Maxwell's fourth equation.

(v) Lorentz Force

The vector sum of electric force and magnetic force on any charged particle is called the Lorentz force.

F⃗ = q[E⃗ + (v⃗ × B⃗)]

The above five equations give a complete description of all electromagnetic interactions.

Do Check - Current Electricity

PRODUCTION OF ELECTROMAGNETIC WAVES

(i) Maxwell's Theory

According to Maxwell, an accelerated charge sets up a magnetic field in its neighbourhood. The magnetic field, in turn, produces an electric field in that region. Both these fields vary with time and act as sources for each other.

(ii) Oscillating Charge

As oscillating charge is accelerated continuously, it will radiate electromagnetic waves continuously.

(iii) Hertz's Demonstration (1888)

In 1888, Hertz demonstrated the production of electromagnetic apparatus is shown schematically in fig.

Hertz's Apparatus:

Input → Transmitter (+/-) → Receiver

Induction coil connected to spherical electrodes

(iv) Transmitter Operation

An induction coil is connected to two spherical electrodes with a narrow gap between them. It acts as a transmitter. The coil provides short voltage surges to the spheres making one positive and the other negative. A spark is generated between the spheres when the voltage between them reaches the breakdown voltage for air. As the air in the gap is ionised, it conducts more rapidly and the discharge between the spheres becomes oscillatory.

(v) LC Circuit Equivalent

The above experiment arrangement is equivalent to an LC circuit, where the inductance is that of the loop and the capacitance is due to the spherical electrodes.

(vi) Wave Radiation

Electromagnetic waves are radiated at very high frequency (100 MHz) as a result of oscillation of free charges in the loop.

(vii) & (viii) Detection

• Hertz was able to detect these waves using a single loop of wire with its own spark gap (the receiver)
• Sparks were induced across the gap of the receiving electrodes when the frequency of the receiver was adjusted to match that of the transmitter

HISTORY OF ELECTROMAGNETIC WAVES

(i) 1865 - Maxwell's Prediction

In year 1865, Maxwell predicted the electromagnetic waves theoretically. According to him, an accelerated charge sets up a magnetic field in its neighborhood.

(ii) 1887 - Hertz's Production

In 1887, Hertz produced and detected electromagnetic waves experimentally at wavelength of about 6m.

(iii) J.C. Bose's Contribution

Seven year later, J.C. Bose became successful in producing electromagnetic waves of wavelength in the range 5 mm to 25 mm.

(iv) 1896 - Marconi's Discovery

In 1896, Marconi discovered that if one of the spark gap terminals is connected to an antenna and the other terminal is earthed, the electromagnetic waves radiated could go upto several kilometers.

(v) Antenna System

The antenna and the earth wires form the two plates of a capacitor which radiates radio frequency waves. These waves could be received at a large distance by making use of an antenna earth system as detector.

(vi) 1899 - First Wireless Communication

Using these arrangements; in 1899 Marconi first established wireless communication across the English channel i.e. across a distance of about 50 km.

PROPERTIES OF ELECTROMAGNETIC WAVES

(i) Wave Equations

The electric and magnetic fields satisfy the following wave equations, which can be obtained from Maxwell's third and fourth equations.

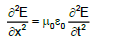
(ii) Speed of Light

Electromagnetic waves travel through vacuum with the speed of light c, where

c = 1/√(μ₀ε₀) = 3 × 10⁸ m/s

(iii) Transverse Nature

The electric and magnetic fields of an electromagnetic wave are perpendicular to each other and also perpendicular to the direction of wave propagation. Hence, these are transverse waves.

(iv) Relationship between E and B

The instantaneous magnitude of E⃗ and B⃗ in an electromagnetic wave are related by the expression

E/B = c

(v) Energy Flow - Poynting Vector

Electromagnetic waves carry energy. The rate of flow of energy crossing a unit area is described by the Poynting vector S⃗

where

S⃗ = (1/μ₀)(E⃗ × B⃗)

(vi) Radiation Pressure

Electromagnetic waves carry momentum and hence can exert pressure (P) on surfaces, which is called radiation pressure. For a perfectly absorbing surface

P = S/c

and if incident on a perfectly reflecting surface

P = 2S/c

(vii) Sinusoidal Wave Representation

The electric and magnetic fields of a sinusoidal plane electromagnetic wave propagating in the positive x-direction can also be written as

E⃗ = E_m sin(kx - ωt)

B⃗ = B_m sin(kx - ωt)

where ω is the angular frequency of the wave and k is wave number which are given by

ω = 2πf and k = 2π/λ

(viii) Intensity

The intensity of a sinusoidal plane electromagnetic wave is defined as the average value of Poynting vector taken over one cycle.

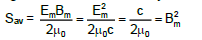
(ix) Fundamental Sources

The fundamental sources of electromagnetic waves are accelerating electric charges. For example radio waves emitted by an antenna arise from the continuous oscillations (and hence acceleration) of charges within the antenna structure.

(x) Superposition Principle

Electromagnetic waves obey the principle of superposition.

(xi) Light Vector

The electric vector of an electromagnetic field is responsible for all optical effects. For this reason electric vector is called a light vector.

Illustration 6: DIn an electromagnetic wave, the amplitude of electric field is 1V/m. The frequency of wave is 5 × 10¹⁴ Hz. The wave is propagating along z-axis. The average energy density of electric field, in Joule/m³, will be:

Options:

(A) 1.1 × 10⁻¹¹

(B) 2.2 × 10⁻¹²

(C) 3.3 × 10⁻¹³

(D) 4.4 × 10⁻¹⁴

Solution:

(B) Average energy density is given by

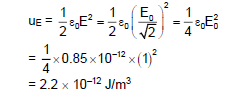
Illustration 7: To establish an instantaneous displacement current of 2A in the space between two parallel plates of 1μF capacitor, the potential difference across the capacitor plates will have to be changed at the rate of:

Options:

(A) 4 × 10⁴ V/s

(B) 4 × 10⁶ V/s

(C) 2 × 10⁴ V/s

(D) 2 × 10⁶ V/s

Solution: (D)

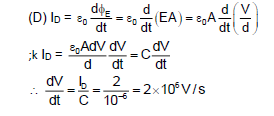
ELECTROMAGNETIC SPECTRUM

(i) Definition

The orderly distribution of electromagnetic waves (on the basis of wavelength or frequency) in the form of distinct groups having widely differing properties is called the electromagnetic spectrum.

The following table gives a complete and detailed picture of electromagnetic spectrum

(ii) Various parts of electromagnetic spectrum

S. No.	Radiation	Discoverer	How produced	Wavelength range	Frequency range	Energy range	Properties	Application
1.	γ-Rays	Henry Becquerel and Madam Curie	Due to decay of radioactive nuclei	10⁻¹⁴ m to 10⁻¹⁰ m	3 × 10²² Hz to 3 × 10¹⁸ Hz	10⁷eV – 10⁴ eV	(a) High penetrating power (b) Uncharged (c) Low ionising power	(a) Gives information on nuclear structure (b) Medical treatment etc.
2.	X-Rays	Roentgen	Due to collisions of high energy electrons with heavy targets	6 × 10⁻¹⁰ m to 10⁻⁹ m	5 × 10¹⁹ Hz to 3 × 10¹⁷ Hz	2.4 × 10⁵ eV to 1.2 × 10³ eV	(a) Low penetrating power (b) Other properties similar to γ-rays except wavelength	(a) Medical diagnosis and treatment (b) Study of crystal structure (c) Industrial radiography
3.	Ultraviolet Rays	Ritter	By ionised gases, sun lamp spark etc.	6 × 10⁻¹⁰ m to 3.8 × 10⁻⁷ m	3 × 10¹⁷ Hz to 5 × 10¹⁹ Hz	2×10³ eV to 3eV	(a) All properties similar to visible light (b) Photo-electric effect	(a) To detect adulteration (b) Sterilization of water due to its destructive action on bacteria
4.	Visible Light	Newton	Outer orbit electron transitions in atoms, gas discharge tube, incandescent	3.8 × 10⁻⁷ m to 7.8 × 10⁻⁷ m	8 × 10¹⁴ Hz to 4 × 10¹⁴ Hz	3.2 eV to 1.6eV	(a) Sensitive to human eye	(a) To see objects (b) To study molecular structure
-	(a) Violet	-	-	3.9×10⁻⁷ m to 4.55×10⁻⁷ m	7.69×10¹⁴ Hz to 6.59×10¹⁴ Hz	-	-	-
-	(b) Blue	-	-	4.55×10⁻⁷ m to 4.92×10⁻⁷ m	6.59×10¹⁴ Hz to 6.10×10¹⁴ Hz	-	-	-
-	(c) Green	-	-	4.92×10⁻⁷ m to 5.77×10⁻⁷ m	6.10×10¹⁴ Hz to 5.20×10¹⁴ Hz	-	-	-
-	(d) Yellow	-	-	5.77×10⁻⁷ m to 5.97×10⁻⁷ m	5.20×10¹⁴ Hz to 5.03×10¹⁴ Hz	-	-	-
-	(e) Orange	-	-	5.97×10⁻⁷ m to 6.22×10⁻⁷ m	5.03×10¹⁴ Hz to 4.82×10¹⁴ Hz	-	-	-
-	(f) Red	-	-	6.22×10⁻⁷ m to 7.80×10⁻⁷ m	4.82×10¹⁴ Hz to 3.84×10¹⁴ Hz	-	-	-
5.	Infra-Red waves	William Herschel	(a) Rearrangement of outer orbitals electrons in atoms and molecules (b) Change of molecular vibrational and rotational energies (c) By bodies at high temperature	7.8×10⁻⁷ m to 10⁻³ m	4×10¹⁴ Hz to 3×10¹¹ Hz	1.6 eV to 1.6×10⁻³ eV	(a) Thermal effect (b) All properties similar to those of light except wavelength	(a) Used in industry, medicine and astronomy (b) Used for fog or have photography
6.	Microwaves	Hertz	Special electronic devices such as klystron tube	10⁻³ m to 0.3m	3×10¹¹ Hz to 10⁹ Hz	10⁻³eV to 10⁻⁵eV	(a) Phenomena of reflection, refraction and diffraction	(a) Radar and telecommunication (b) Analysis of fine details of molecular structure
7.	Radio waves	Marconi	Oscillating circuits	0.3m to few kms	10⁹ Hz to few Hz	10⁻³eV to 0	(a) Exhibit wave like properties more than particle like properties	(a) Radio communication (b) Radar, Radio and satellite communication (Microwaves)

Subparts of Radio spectrum

Type	Wavelength	Frequency	Applications
(a) Super High (SHF)	0.01m to 0.1m	3×10¹⁰ Hz to 3×10⁹ Hz	Radar and television broadcast
(b) Ultra High (UHF)	0.1m to 1m	3×10⁹ Hz to 3×10⁸ Hz	Short distance communication
(c) Very High (VHF)	1m to 10m	3×10⁸ Hz to 3×10⁷ Hz	Television communication
High frequency	10m to 100m	3×10⁷ Hz to 3×10⁶ Hz	Medium distance communication
Medium frequency	100m to 1000m	3×10⁶ Hz to 3×10⁵ Hz	Marine and navigation use
Low Frequency	1000m to 10000m	3×10⁵ Hz to 3×10⁴ Hz	Long range communication
Very low frequency	10000m to 30000m	3×10⁴ Hz to 10³ Hz	Long distance communication

EARTH'S ATMOSPHERE AND ELECTROMAGNETIC WAVES

(i) Earth's Atmosphere

The gaseous envelop surrounding the earth is called earth's atmosphere.

(ii) Composition

It mainly consists of nitrogen 78% and oxygen 21% alongwith a little portion of argon, carbon-di-oxide, water vapour, hydrocarbons, sulphur compounds and dust particles.

(iii) Density Variation

The density of atmospheric air goes on decreasing gradually as we go up.

(iv) Atmospheric Layers

The earth's atmosphere has no sharp boundary. However, it has been divided into various regions as given below:

• (a) Troposphere

It extends upto a height of 12 km from earth's surface. The temperature in this region decreases from 298K to 220K and conductivity increases. All climatic changes occur in this region.

• (b) Stratosphere

It extends from 12 km to 50 km after troposphere. At the upper part of this region, approximately 20km thick, most of ozone of atmosphere is concentrated. This layer is called as ozone layer. This layer absorbs very large portion of ultraviolet radiations coming from sun, therefore its temperature increases from 220K to 280K.

• (c) Mesosphere

It extends from 50km to 80 km after stratosphere. In this region the temperature decreases from 280K to 180K

• (d) Ionosphere

It extends from 80 km to 400 km after mesosphere. The temperature of this region rises from 180K to 700K. In this region ultraviolet radiation coming from sun cause ionisation, therefore this part mostly consists of free electrons and positive ions. The concentration of free electrons is found to be very large in a region beyond 110 km from earth's surface which extends vertically for a few kilometers and is called Kennelly Heaviside layer. Beyond this layer the concentration of free electrons decreases considerably until a height of about 250 km. Beyond it there is another layer of electrons, called Appleton layer.

(v) Greenhouse Effect

The atmosphere is transparent to visible radiations, but most infrared (heat) radiations are not allowed to pass through. The energy from the sun heats the earth which then starts emitting radiations like any other hot body. However, since the earth is much colder than sun, its radiations are mainly in the infra red region. These radiations are unable to cross the lower atmosphere and are reflected back. Low lying clouds also reflect back the infra red radiations. As such, the earth's surface warm at night. This phenomenon is called the Green house effect.

(vi) Propagation of Radio waves

• (a) Low frequency waves - the AM band

Radio waves having wavelengths of 10m or more (frequency less than 30 MHz) are said to constitute the AM band. The lower atmosphere is transparent to these waves, but the ionosphere reflects them back. A signal transmitted from a certain point can be received at another point in two possible ways - directly along the surface of the earth (called ground wave) and after reflection from ionosphere (called sky wave). Waves having frequencies upto about 1500kHz (Wavelength above 200m) are mainly transmitted through ground because low frequency sky waves lose their energy very quickly than the sky waves. Therefore, higher frequencies are mainly transmitted through sky. These two regions of the AM band are called medium wave and short wave bands respectively.

• (b) High frequency waves - Television transmission

Above a frequency of about 40MHz the ionosphere does not reflect the wave toward the earth. The television signals have frequencies in the range 100-200 MHz. Therefore TV transmission via the sky is not possible - only direct reception via the ground is possible. Therefore, in order to have larger coverage, the transmission has to be done through very tall antennas. The height of transmitting antenna for TV telecast is given by

h = d²/(2R_e)

where d is the radius of the area to be covered for TV telecast and R_e is the radius of earth.

Illustration 8: A T.V. tower has a height of 100m. How much population is covered by T.V. broadcast, if the average population density around the tower is 1000/km²?

Options:

(A) 39.5 × 10⁵

(B) 19.5 × 106

(C) 29.5 × 107

(D) 9 × 104

Solution:

(A) Radius of the area covered by T.V. telecast

d = √(2hR_e)

Total population covered = πd² × population density

= 2πhR_e × population density = 2 × 3.14 × 100 × 6.4 × 10⁶ × (1000/10⁶) = 39.503 × 10⁵

Illustration 9: An electromagnetic radiation has an energy 14.4 KeV. To which region of electromagnetic spectrum does it belong?

Options:

(A) Infra red region

(B) Visible region

(C) X-ray region

(D) Y-ray region

Solution: