Wave and Sound

Wave motion and sound represent fundamental concepts in physics that govern how energy travels through various media without the transport of matter itself. These phenomena are essential to understanding everything from musical instruments to modern communication systems, making them crucial topics for physics students and educators alike.

What is Wave Motion?

Wave motion occurs when a disturbance in an elastic medium propagates from one point to another, transferring energy without transporting the particles of the medium. When a portion of an elastic medium is displaced from its equilibrium position, it begins oscillating and transmits this disturbance to neighboring particles due to the medium's elastic properties.

The key characteristic that distinguishes waves from other forms of energy transfer is that energy travels from one location to another without any particles moving between those two points. This fundamental principle underlies all wave phenomena, from water waves on a pond to electromagnetic radiation traveling through space.

Essential Wave Properties and Characteristics

Amplitude, Frequency, and Phase

Amplitude represents the maximum displacement of particles from their equilibrium positions and determines the energy carried by the wave. In sound waves, amplitude correlates with loudness, while in light waves, it relates to intensity.

Frequency measures how many complete oscillations occur per second, expressed in Hertz (Hz). This property remains constant as a wave travels through different media, making it a fundamental characteristic of the wave source.

Phase describes the state of motion of particles in the medium at any given time. Particles are "in phase" when they have identical displacement and velocity at the same instant, while "out of phase" particles have different states of motion.

Wavelength represents the minimum distance between particles vibrating in the same phase, effectively measuring one complete wave cycle in space.

Types of Waves: Longitudinal vs. Transverse

Understanding wave classification is crucial for analyzing different physical phenomena:

Longitudinal waves occur when particles oscillate parallel to the direction of wave propagation. Sound waves in air exemplify this type, with particles moving back and forth along the same direction the sound travels, creating regions of compression and rarefaction.

Transverse waves feature particle oscillations perpendicular to the wave's direction of travel. Examples include waves on a string, water surface waves, and electromagnetic radiation. These waves can exhibit polarization, a property exclusive to transverse waves.

Wave Equations and Mathematical Description

The mathematical representation of wave motion provides precise tools for analyzing wave behavior. For a sinusoidal wave traveling in the positive x-direction, the displacement equation is:

Where:

• y = particle displacement
• a = amplitude
• ω = angular frequency (2πf)
• k = wave number (2π/λ)
• t = time
• x = position

This equation reveals that wave motion depends on both spatial (x) and temporal (t) variables, with the negative sign indicating rightward propagation.

Standing Waves and Resonance Phenomena

Standing waves form when two identical waves traveling in opposite directions interfere. Unlike traveling waves, standing waves create stationary patterns with fixed nodes (zero amplitude) and antinodes (maximum amplitude).

The distance between consecutive nodes or antinodes equals λ/2, while the distance between a node and adjacent antinode is λ/4. These patterns are fundamental to musical instruments, where string length determines the resonant frequencies that produce musical notes.

For a string fixed at both ends, the fundamental frequency is:

Where L is string length, T is tension, and μ is linear mass density.

Sound Waves and Acoustic Properties

Sound represents longitudinal mechanical waves that require a medium for propagation. In gases like air, sound creates alternating compressions and rarefactions as particles oscillate about their equilibrium positions.

The speed of sound in air depends on temperature and is given by:

Where γ is the heat capacity ratio, R is the gas constant, T is absolute temperature, and M is molar mass.

At standard conditions (20°C), sound travels at approximately 343 m/s in air, though this increases with temperature due to enhanced molecular motion.

The Doppler Effect in Wave Motion

The Doppler effect describes the apparent frequency change when there's relative motion between the wave source and observer. This phenomenon is observable in everyday situations, from the changing pitch of passing ambulances to astronomical observations of stellar motion.

For sound waves, the observed frequency is:

Where the upper signs apply when source and observer approach each other, and lower signs when they move apart.

Interference and Beats

When two or more waves occupy the same region simultaneously, they interfere according to the superposition principle. Constructive interference occurs when waves are in phase, producing amplified resultant waves. Destructive interference happens when waves are out of phase, potentially canceling each other completely.

Beats result from the interference of two waves with slightly different frequencies, producing a periodic variation in amplitude. The beat frequency equals the absolute difference between the component frequencies:

Key Wave and Sound Formulas Reference

Formula Name	Mathematical Expression	Description
Wave Equation	y = a sin(ωt - kx)	General sinusoidal wave traveling rightward
Wave Speed	v = fλ	Fundamental relationship between frequency and wavelength
Wave Number	k = 2π/λ	Spatial frequency of the wave
Standing Wave	y = 2a sin(kx) cos(ωt)	Resultant of two identical opposing waves
String Frequency	f = (1/2L)√(T/μ)	Fundamental frequency of stretched string
Sound Speed (Air)	v = √(γRT/M)	Speed of sound in ideal gas
Doppler Effect	f' = f(v ± vo)/(v ± vs)	Apparent frequency due to relative motion
Beat Frequency	fbeat = |f1 - f2|	Frequency of amplitude modulation
Sound Intensity	I = (1/2)ρvω2A2	Energy flux per unit area
Decibel Scale	β = 10 log10(I/I0)	Logarithmic intensity measurement
Open Pipe Frequency	f = nv/2L	Resonant frequencies in open tubes
Closed Pipe Frequency	f = (2n-1)v/4L	Resonant frequencies in closed tubes

This comprehensive understanding of wave motion and sound provides the foundation for advanced topics in acoustics, optics, and modern physics, making these concepts essential for any serious study of physical sciences.

WAVE MOTION

A wave originates due to displacement of some portion of an elastic medium from its normal position, causing it to oscillate about an equilibrium position. Because of the elastic properties of the medium, the disturbance is transmitted from one particle to another. Such a progressing disturbance is called a wave.

A wave allows energy to be transferred from one point to another some distance away without any particles of the medium travelling between the two points.

CONCEPTS OF AMPLITUDE, FREQUENCY AND PHASE

(i) Amplitude

The modulus of the maximum displacement of the particles of the medium from their respective equilibrium positions.

(ii) Frequency

The number of oscillations performed by the particles of the medium in one second.

(iii) Phase

The state of motion of the particles of the medium is called the phase of a wave.

(iv) Wavelength

The minimum distance between particles where particles vibrate in the same phase.

Longitudinal And Transverse Waves

In a longitudinal wave the particles of a medium conveying a mechanical wave moves back and forth along the direction of propagation. Sound in air is a longitudinal wave.

In a transverse wave the particles of the medium oscillate in the direction perpendicular to the direction of propagation.

Equation of a Wave

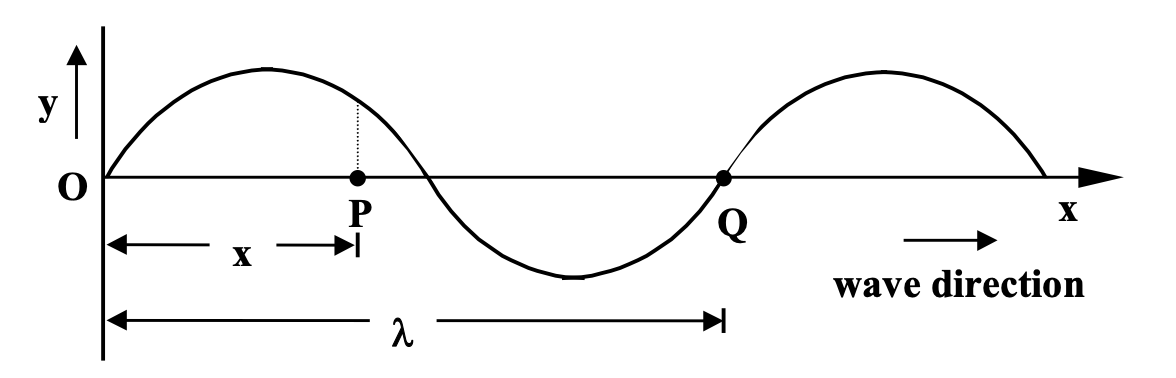
Suppose a wave moves from left to right and that a particle at the origin O then vibrates according to the equation:
y = a sin(ωt), where t is the time and ω = 2πf.

At a point P which is at a distance x from O to the right, the phase of the vibration will be different from that at O. The particle Q at a distance λ from O lags by angle 2π. Therefore the point P lags point O in phase by:

φ = (2π/λ) x

Thus, the displacement of the particle P is given by:

y = a sin(ωt - φ)

or

y = a sin(ωt - (2π/λ) x)

Since ω = 2πf = 2π(v/λ), where v is the velocity of the wave, the equation of the wave may be written as.

Wave Equation

y = a sin ( ^2πvt⁄_λ – ^2π⁄_λ x )

or

y = a sin ^2π⁄_λ ( vt – x )

or

y = a sin( ωt – kx ) where k = ^2π⁄_λ

The negative sign in the bracket indicates that the wave moves from left to right, the vibrations at point P will lag from that of the point O. When the waves travel from right to left, it will arrive at P before O. Thus the vibration at P leads that at O. Consequently, the wave equation is

y = a sin( ωt + kx )

Wave Function Condition

Differentiating equation twice with respect to time. We obtain d²y/dt² = v² d²y/dx²

Superposition of Wave 

All types of waves, mechanical as well as electromagnetic, are, in general, subject to the principle of superposition. According to the principle of superposition, if two or more independent waves are propagated through a medium or space, all at, the same time, the resultant physical quantity (i.e. displacement, velocity, acceleration, etc.) at any point is the vector sum of the quantities due to each individual wave.

Thus, in the case of one dimensional or plane waves, the resultant displacement at any point is the linear sum of the displacements due to the individual.

Interference

When two sound waves of the same frequency, (preferably of the same amplitude) and having constant initial phase difference superimpose each other, the effect of one wave is permanently cancelled by the other producing permanent silence at that point, or the effect of one wave is reinforced by the other permanently producing maximum sound at that point. This phenomenon of either permanent cancellation or reinforcement of two sound waves is respectively called destructive and constructive interference.

The interference of two sound waves with identical wavelengths passing through a common point depends on their phase difference δ. If the waves were emitted in phase, δ is given by

δ = (2π/λ) p

where p is the path length difference (the difference in the distances travelled by the waves to reach the common point).

Conditions for constructive and destructive interference of the waves are given by

δ = n(2π); n = 0, 1, 2, ………… (constructive interference)

or
p = nλ

and

δ = (n + 1/2) 2π; n = 0, 1, 2, …… (destructive interference)

or
p = (n + 1/2) λ

If I₁ and I₂ are intensities of the interfering waves and δ is the phase difference, then the resultant intensity is given by

I = I₁ + I₂ + 2√(I₁ I₂) cos δ

Now,

I_max = (√I₁ + √I₂)² for δ = 2nπ

I_min = (√I₁ − √I₂)² for δ = (n + 1/2) 2π

Standing Waves

A standing wave is formed when two identical waves travelling in the opposite directions along the same line, interfere. On the path of a stationary wave, the amplitude of vibration varies simple harmonically with respect to the distance from one end of the path.

On the path of the stationary wave, there are points where the amplitude is zero, they are known as NODES. On the other hand there are points where the amplitude is maximum, they are known as ANTINODES.

The distance between two consecutive nodes or two consecutive antinodes is λ/2.

The distance between a node and the next antinode is λ/4.

Consider two waves of the same frequency, speed and amplitude which are travelling in opposite directions along a string. Two such waves may be represented by the equations:

y₁ = a sin(kx - ωt)
y₂ = a sin(kx + ωt)

Hence the resultant may be written as:

y = y₁ + y₂ = a sin(kx - ωt) + a sin(kx + ωt)
y = 2a sin(kx) cos(ωt)

This is the equation of a standing wave.

NOTE :

(i) In this equation, it is seen that a particle at any particular point ‘x’ executes simple harmonic motion and all particles vibrate with the same frequency.

(ii) The amplitude is not the same for different particles but varies with the location ‘x’ of the particle.

(iii) The points having maximum amplitudes are those for which 2a sin kx has a maximum value of 2a; these are at the positions,
 kx = π/2, 3π/2, 5π/2, …
 or x = λ/4, 3λ/4, 5λ/4, …
These points are called antinodes. The strain is minimum at these points.

(iv) The amplitude has minimum value of zero at positions where
 kx = π, 2π, 3π, …
 or x = λ/2, λ, 3λ/2, 2λ, …
These points are called nodes. The strain is maximum at these points.

(v) Energy is not transported along the string to the right or to the left, because energy cannot flow past the nodal points in the string which are permanently at rest.

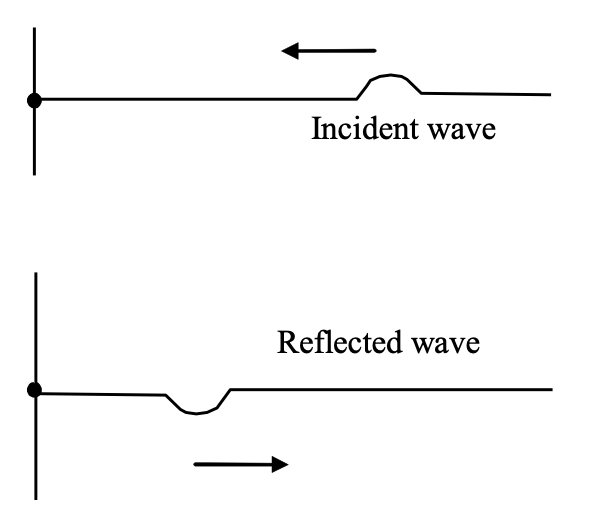
Reflection of Waves

(a) Waves on reflection from a fixed end undergoes a phase change of 180°.

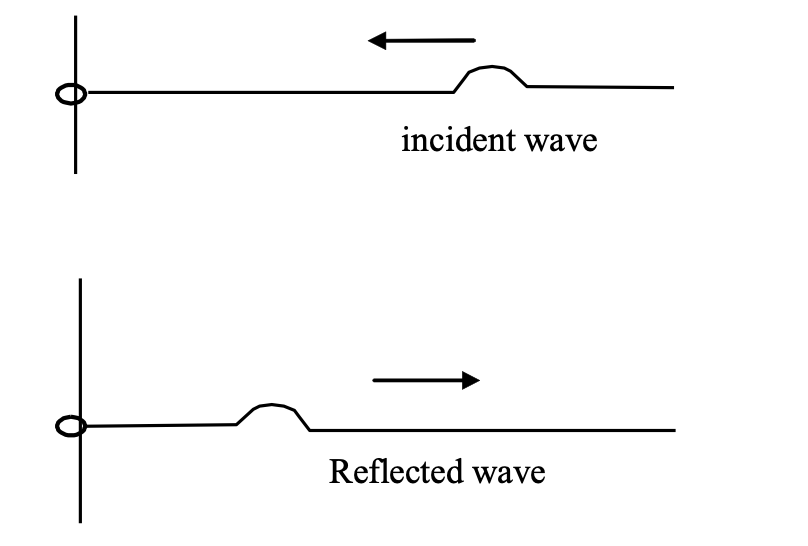
(b) While a wave reflected from a free end is reflected without a change in phase.

Stationary Waves in Strings

A string of length L is stretched between two points. When the string is set into vibrations, a transverse progressive wave begins to travel along the string. It is reflected at the other fixed end. The incident and the reflected waves interfere to produce a stationary transverse wave in which the ends are always nodes.

(a) In the simplest form, the string vibrates in one loop in which the ends are the nodes and the centre is the antinode. This mode of vibration is known as the fundamental mode and the frequency of vibration is known as the fundamental frequency or first harmonic.

Since the distance between consecutive nodes is λ/2

Since the distance between consecutive nodes is λ₁/2,

L = λ₁/2 ∴ λ₁ = 2L

If f₁ is the fundamental frequency of vibration, then the velocity of transverse waves is given as,
v = λ₁ f₁ or v = 2L f₁ . . . (1)

(b) The same string under the same conditions may also vibrate in two loops, such that the centre is also the node.

∴ L = 2 × (λ₂/2) ∴ λ₂ = L

If f₂ is the frequency of vibrations, then the velocity of transverse waves is given as,
v = λ₂ f₂ ∴ v = L × f₂ . . . (2)

The frequency f₂ is known as second harmonic or first overtone.

(c) The same string under the same conditions may also vibrate in three segments.

∴ L = 3 × (λ₃/2) ∴ λ₃ = ²⁄₃ L

If f₃ is the frequency in this mode of vibration, then,
v = λ₃ f₃ ∴ v = ²⁄₃ L f₃ . . . (3)

The frequency n₃ is known as the third harmonic or second overtone. Thus a stretched string, in addition to the fundamental mode, also vibrates with frequencies which are integral multiples of the fundamental frequency. These frequencies are known as harmonics.

The velocity of transverse waves in a stretched string is given as

v = √(T/μ) where T = tension in the string.

μ = linear density or mass per unit length of string.

If the string, fixed at two ends, vibrates in its fundamental mode, then

v = 2 L f ∴ f = (1 / 2L) √(T/μ)

μ = volume of unit length × density

= πr² × 1 × ρ = π × (D²/4) × ρ where D = diameter of the wire, ρ = density.

Note:

If the ratio of two frequencies f₁/f₂ is 1, then they are to be in unison.

If f₁/f₂ = 2, then f₁ is the upper octave of f₂.

If f₁/f₂ = 1/2, then f₁ is the lower octave of f₂.

Stationary Waves in AIR column

Open Pipe

If both ends of a pipe are open and a system of air is directed against an edge, standing longitudinal waves can be set up in the tube. The open end is a displacement antinode.

1. For fundamental mode of vibrations,
   L = λ₁/2 ∴ λ₁ = 2L
   v = λ₁ f₁ ∴ v = 2L f₁ … (1)
2. For the second harmonic or first overtone,
   L = λ₂ or λ₂ = L
   v = λ₂ f₂ ∴ v = L f₂ … (2)
3. For the third harmonic or second overtone,
   L = 3 × (λ₃/2) ∴ λ₃ = (2/3) L
   v = λ₃ f₃ ∴ v = (2/3) L f₃ … (3)

From (1), (2) and (3) we get, f₁ : f₂ : f₃ : … = 1 : 2 : 3 : …
i.e. for a cylindrical tube, open at both ends, the harmonics excitable in the tube are all integer multiples of its fundamental.

∴ In the general case, λ = 2L/n where n = 1, 2, …

Frequency = v/λ = nv/2λ  where n = 1, 2

Closed Pipe

If one end of a pipe is closed the reflected wave is 180° out of phase with the wave. Thus the displacement of the small volume elements at the closed end must always be zero. Hence the closed end must be a displacement node.

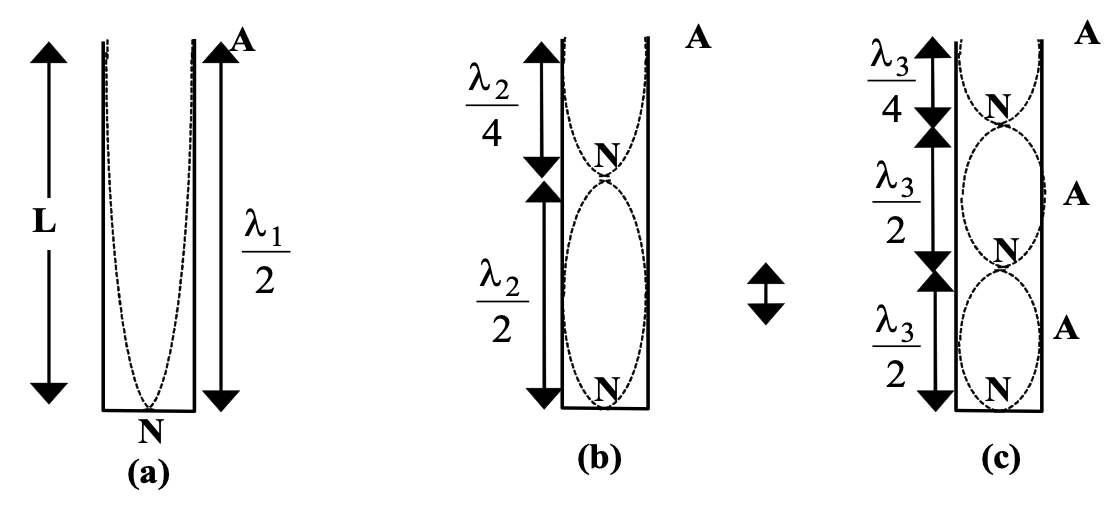
(a) This represents the fundamental mode of vibration.

L = λ₁/4 ∴ λ₁ = 4L

If f₁ is the fundamental frequency, then the velocity of sound waves is given as,

v = λ₁ f₁ ∴ v = 4L f₁ ... (1)

(b) This is the third harmonic or first overtone.

L = 3 × λ₂/4 ∴ λ₂ = 4/3 L

v = λ₂ f₂ ∴ v = (4/3) L f₂ ... (2)

(c) This is the fifth harmonic or second overtone.

L = 5 × λ₃/4 ∴ λ₃ = 4/5 L

v = λ₃ f₃ ∴ v = (4/5) L f₃ ... (3)

From (1), (2) and (3) we get,

f₁ : f₂ : f₃ : ....... = 1 : 3 : 5 : .......

In the general case, λ = 4l/(2n+1) where n = 0, 1, 2, ......

Velocity of sound = v

Frequency = ((2n+1) v) / 4l where n = 0, 1, 2, ....

Note : The antinode formed at the open end is not exactly at that point but shifted away from pipe by distance 0.6R (where R is radius of cross-section of pipe). This is called "end correction".

Beats

When two waves of slightly different frequencies travel through the same region, then the amplitude of the resultant wave at any given point is not constant but varies in time. In case of sound the varying amplitude gives rise to variations in loudness which are called beats.

Let the displacement produced at a point by one wave be
y₁ = a cos(2π f₁ t)

and the displacement produced at the point by the other wave of equal amplitude as
y₂ = a cos(2π f₂ t)

By the principle of superposition, the resultant displacement is
y = y₁ + y₂ = a[cos(2π f₁ t) + cos(2π f₂ t)]

= 2a cos[2π((f₁ − f₂)/2) t] cos[2π((f₁ + f₂)/2) t]

Beat frequency = f₁ − f₂ (assuming f₁ > f₂)

WAVE SPEED

The speed of any mechanical wave, transverse or longitudinal depends on both inertial property of the medium (to store kinetic energy) and on elastic property of the medium (to store potential energy).

Transverse Wave in a Stretched String

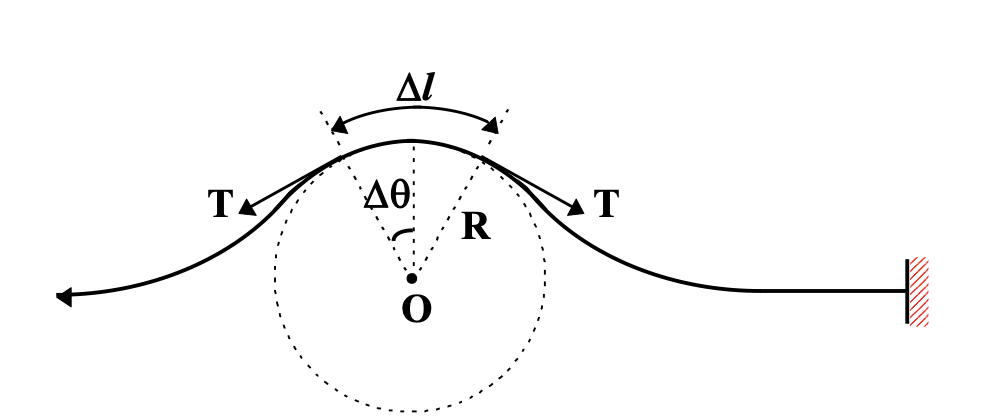
Consider a transverse pulse produced in a taut string of linear mass density μ. Consider a small segment of the pulse, of length Δl, forming an arc of a circle of radius R. A force equal in magnitude to the tension T pulls tangentially on this segment at each end.

The net restoring force on the element is

F = 2Tsin(θ) ≈ T(2θ) = T (Δl / R)

The mass of the segment is μΔl.

The acceleration of this element toward the centre of the circle is

a = v² / R , where v is the velocity of the pulse.

Using second law of motion,

T (Δl / R) = (μΔl)(v² / R)

or

v = √(T / μ)

Longitudinal Wave In Fluids

Sound wave in air is a longitudinal wave. As a sound wave passes through air, potential energy is associated with periodic compressions and expansions of small volume elements of the air. The property that determines the extent to which an element of the medium changes its volume as the pressure applied to it is increased or decreased is the bulk modulus B.

B = -ΔpΔVV

where ΔVV is the fractional change in volume produced by a change in pressure Δp.

Velocity of longitudinal wave is given in terms of elasticity and density of the medium as

v = Bρ

Sound Waves

The longitudinal waves in air which on striking the ear give rise to the sensation of sound, are called sound waves. The simplest sound waves are sinusoidal or like a sine curve. When such a wave arrives at the ear, it causes a vibration of the air particles at the eardrum with a definite frequency and amplitude. This vibration may also be described in terms of the variation of air pressure at the same point. The air pressure rises above atmospheric pressure, and then drops below atmospheric pressure, with simple harmonic motion of the same frequency as that of an air particle.

Longitudinal Wave Equations

The sinusoidal longitudinal wave in air may be represented as :

y = A sin(ωt - kx)

Where y is the longitudinal displacement from the equilibrium position.

The variation of pressure is given by

p = -B ∂y/∂x

or

p = BkA cos(ωt - kx) = p_m cos(ωt - kx)

or

p_m = BkA

Sound Intensity

The intensity I of a sound wave is the average rate at which it transmits energy through a unit area and is found as

I = (1/2) ρ v ω² A²

Since
v = √(B/ρ) , therefore I = (1/2) ρ B k A²

or
I = (1/2) ρ B k (p_m / Bk)² = (1/2) v p_m² / B ( ∴ p_m = B k A )

Also,
I = p_m² / (2 ρ v) = p_m² / (2 √(ρB))

Sound Level in Decibels.

The sound level L in decibels (dB) is defined as

L = 10 log ( I / I₀ ) (dB)

Where I₀ = 10^-12 W/m² is the reference intensity level to which any intensity I is compared.

Velocity of sound in AIR

Newton's Formula

Newton assumed that the propagation of sound waves in a gas is an isothermal (constant temperature) process so that Boyle's law holds. Thus for a given mass of gas at pressure P and volume V, we have

PV = constant

Differentiating:

P dV + V dP = 0

P = - dP / (dV/V)

But, Bulk modulus k of the gas B = - dP / (dV/V)

Hence v = √(P / ρ)

Hence, for air at NTP and density ρ = 1.29 kg/m^-3
v = 280 m/s

Newton's formula is not valid because experimental value is 332 m/s.

Laplace's Correction

Laplace pointed out that gases are bad conductors of heat, and the compressions and rarefaction occur very rapidly. Therefore the heat developed at compression cannot go to the surroundings, and the heat disappeared at rarefaction cannot come in from the surroundings. So the air in the path of a sound wave suffer temperature changes i.e. the conditions are adiabatic rather than isothermal.

Hence, in the case of an ideal gas, the relation between pressure p and volume V during an adiabatic process is given by

PV^γ = constant

Where γ is the ratio of the heat capacity at constant pressure to that at constant volume.

After differentiating, we get

dPdVVγ + γPVγ-1 = 0

Since

B = -V dPdV = γP

∴ v = √(γP / ρ)

Using the gas equation

Pρ = RTM

where M is the molar mass.

Thus,

v = √(γRT / M)

Doppler Effect

The apparent shift in frequency of the wave motion when the source of sound or light moves with respect to the observer, is called Doppler Effect.

Calculation of Apparent Frequency.

Suppose v is the velocity of sound in air, v_s is the velocity of the source of sound(s), v_o is the velocity of the observer (O), and f is the frequency of the source.

(i) Source moves towards stationary observer.
If the source were stationary the f waves sent out in one second towards the observer O would occupy a distance v, and the wavelength would be v/f.

If S moves with a velocity v_s towards O, the f waves sent out occupy a distance (v − v_s) because S has moved a distance v_s towards O in 1 s. So the apparent wavelength would be

λ′ = (v − v_s) / f

Thus, apparent frequency f′ =

Velocity of sound relative to O / Wavelength of wave reaching O

f′ = v / λ′ = f ( v / (v − v_s) )

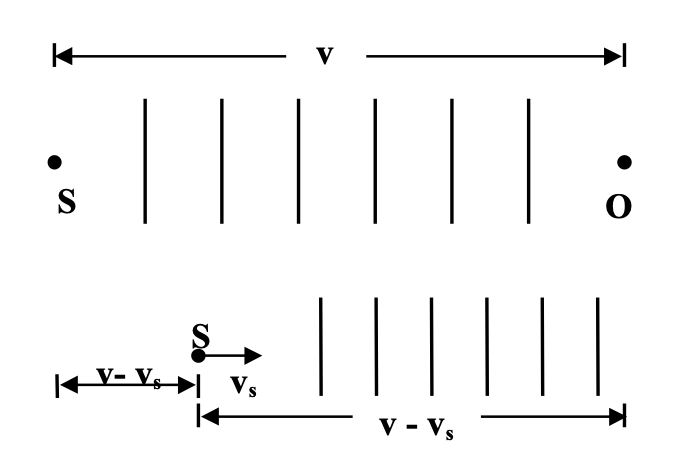
(ii) Source moves away from stationary observer.

Now, apparent wavelength

λ' = (v + v_s) / f

∴ Apparent frequency f' = v / λ'
or f' = f ( v / (v + v_s) )

(iii) Observer moves towards stationary source.

f' = (Velocity of sound relative to O) / (Wavelength of wave reaching O)

Here, velocity of sound relative to O = v + v_o and wavelength of waves reaching O = v / f

∴ f' = (v + v_o) / (v / f) = f ( (v + v_o) / v )

(iv) Observer moves away from the stationary source.

f' = (v - v_o) / (v / f) = f ( (v - v_o) / v )

(v) Source and observer both move toward each other.

f' = (v + v_o) / (v - v_s) × f = f ( (v + v_o) / (v - v_s) )

(vi) Both move away from each other.

f' = f ( (v - v_o) / (v + v_s) )

(vii) Source moves towards observer but observer moves away from source

f = f' ( ^{v - v_o}⁄_{v - vs} )

(viii) Source moves away from observer but observer moves towards source

f = f' ( ^{v + v_o}⁄_{v + vs} )

Wind's Effect

The above formulae can be modified by taking the wind effects into account. The velocity of sound should be taken as v + v_w or v - v_w if the wind is blowing in the same or opposite direction as SO (source to observer).