Electrostatics

Charge is the physical property of certain fundamental particles (like electron, proton) by virtue of which they interact with the other similar fundamental particles. These are solely responsible for electrical interaction as well as magnetic interaction in nature. The study of electrical interaction of charges at rest is referred as electrostatic. To distinguish the nature of interaction, charges are divided into two parts (i) positive (ii) negative. Like charges repel and unlike charges attract.

SI unit of charge: coulomb

CGS unit: esu

1C = 3 × 10⁹ esu

Magnitude of the smallest known charge is e = 1.6 × 10⁻¹⁹C (charge of one electron or proton).

• Note: True test of electrification is repulsion and not attraction as attraction may also take place between a charged and an uncharged body and also between two oppositely charged bodies.

PROPERTIES OF ELECTRIC CHARGE

• QUANTIZATION OF CHARGE

Charge exists in discrete packets rather than in continuous amount.

i.e. charge on any body is the integral multiple of the charge on an electron

Q = ± ne, where n = 0, 1, 2, .................

• Conservation Of Charge

Charge is conserved, i.e. total charge on an isolated system is constant. By isolated system, we mean here a system through the boundary of which no charge is allowed to escape or enter. This does not require that the amount of positive and negative charges separately conserved; only their algebraic sum is.

• Charges on a Conductor

Static charges reside on the surface of the conductor.

• Distribution of Charges

The concentration of the charges is maximum on a surface with greater curvature.

Methods of charging:

• Charging by friction: When two bodies are rubbed with each other, there is a transfer of electrons from one body to other.
• Charging by induction: When a charged body is brought near an uncharged body, there appears a charge on the surface of uncharged body due to attractive/repulsive forces between charges. The induced charge can be lesser or equal to the inducting charge. Its maximum value is given by

  q'/q = 1/(1 + k) where k is the dielectric constant of the material of uncharged body.

COULOMB'S LAW

The force of interaction between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.

• In free space

F = (1/4πε₀) × (q₁q₂/r²)

ε₀ – permittivity of free space (Vacuum)

• In material medium

F = (1/4πε) × (q₁q₂/r²)

ε - permittivity of the medium

Where ε = ε₀εᵣ

εᵣ = relative permittivity of the medium

• In vector form

F⃗ = (1/4πε₀) × (q₁q₂/r³) × r⃗

(1/4πε₀) = 9 × 10⁹ Nm²/C²

ε₀ = 8.854 × 10⁻¹² C²/Nm²

Do Check - Current Electricity

Properties of Coulomb's Law:

1. This is a fundamental law and is based on physical observation
2. The force is an action - reaction pair
3. The direction of force is always along the line joining the two charges
4. The force is conservative i.e. work done by it is independent of path
5. Electrical force between two point charges is independent of presence or absence of other charges

Illustration: A particle 'A' having a charge of 2 × 10⁻⁶C and a mass of 100g is fixed at the bottom of a smooth inclined plane of inclination 30°. Where should another particle B, having same charge and mass be placed on the incline so that it may remain in equilibrium?

Solution:

First of all draw the F.B.D. of the masses.

For equilibrium ΣF = 0

N = mg cos30° ... (1)

Fₑ = mg sin30° ... (2)

From (2): kq²/x² = mg sin30°/2

x = √(2kq²/mg) = 27cm

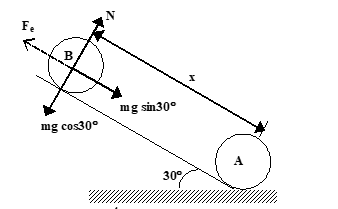
(Here k = 1/4πε₀ = 9 × 10⁹ Nm²/C²)

Electric Field Intensity

It is the force experienced by a unit positive charge placed at a point in an electric field.

E⃗ = lim(q→0) F⃗/q

E⃗ = (1/4πε₀) × (q/r³) × r⃗ [In vacuum or free space]

E = (1/4πε₀) × (q/r²)

Unit: N/C or volt/m

Dimension: [MLT⁻³I⁻¹]

Illustration: Two particles A and B having charges 8 × 10⁻⁶ C and –2 × 10⁻⁶C respectively are held fixed with a separation of 20 cm. Where should a third charged particle be placed so that it does not experience a net electric force?

Solution: As the net electric force on C should be equal to zero, the force due to A and B must be opposite in direction. Hence, the particle should be placed on the line AB. As A and B have charges of opposite signs, C cannot be between A and B.

Also A has larger magnitude of charge than B. Hence, C should be placed closer to B than A. The situation is shown in figure. Suppose BC=x and the charge on C is Q

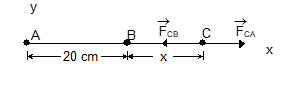
Then:

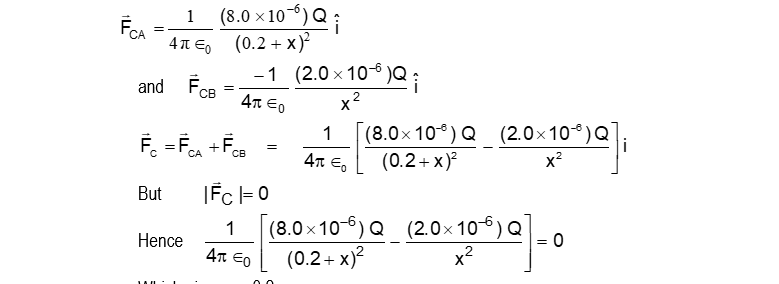
Which gives x = 0.2 m

Superposition principle

Force experienced by a given charge in the field of a number of point charges is the vector sum of all the forces.

F⃗_net = F⃗₁ + F⃗₂ + F⃗₃ + F⃗₄ + ...

Similarly for electric field:

E⃗_net = E⃗₁ + E⃗₂ + E⃗₃ + ...

For continuous distribution of charge:

E⃗ = ∫ dE⃗

Note: Electric field at the geometrical centre of symmetrically and uniformly distributed charge on a regular shaped body is always zero.

Lines of Force

• Lines of force originate from positive charges and terminate on negative charges
• Lines of force originate or terminate perpendicular to the surface
• Tangent to the lines of force at any point gives the direction of the electric field
• Lines of force crossing through any cross-sectional area perpendicular to its direction of flow is proportional to the magnitude of the electric field intensity
• Lines of force do not intersect

Exercise 1:

1. Is it possible to move a charge in an electric field without doing work? If so how and if not why?
2. A certain charge Q is divided into two parts q and Q-q, which are then separated by a certain distance. What must q be in terms of Q to maximize the electrostatic repulsion between the two charges?
3. Does coulomb's law hold for all charged objects?
4. Two identical metallic spheres of exactly equal masses are taken, one is given a positive charge q and the other an equal negative charge. These masses after charging are different. Comment on the statement.

Electric Field Intensity

• Due to a point charge

E = (1/4πε₀) × (q/r²)

• Due to linear distribution of charge

If λ = linear charge density of rod

(i) At a point on its axis.

E = (λ/4πε₀) × [1/a - 1/(L+a)]

(ii) At a point on its Perpendicular axis to one end

Eₓ = (λ/4πε₀) × [1/y - 1/√(y² + L²)]

Eᵧ = (λ/4πε₀) × [L/(y√(y² + L²))]

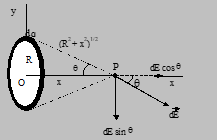
• Due to ring of uniform charge distribution

At a point on its axis

E = (1/4πε₀) × (qx/[x² + a²]³/²)

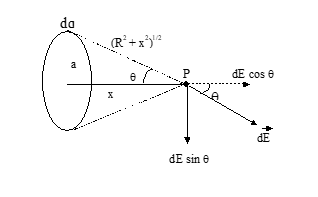
• Due to uniformly charged disc

At a point on its axis.

E = (σ/2ε₀) × [1 - x/√(x² + a²)]

Here, σ – surface charge density

a = radius of disc

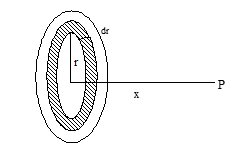
• Due to a shell (hollow sphere)

1. E inside = 0 (r < R)
2. E surface = q/(4πε₀R²) (r = R) Here R= radius of hollow sphere
3. E outside = q/(4πε₀r²) (r > R)

Non conducting solid sphere having uniform volume distribution of charge

(i) Outside point

E = (1/4πε₀) × (q/r²)

(ii) Inside point

E = (1/4πε₀) × (qr/R³)

q = total charge

Cylindrical Conductor of Infinite length

• Outside point

E = λ/(2πε₀r)

• Inside point

E = 0

λ - linear density of charge

(as charges reside only on the surface)

Non-conducting cylinder having uniform volume density of charge

• Outside point

E = λ/(2πε₀r)

• Inside point

E = ρr/(2ε₀)

here, ρ = volume charge density

Infinite plane sheet of charge

E = σ/(2ε₀)

σ – surface charge density

Two oppositely charged sheets (Infinite)

(i) Electric field at points outside the charged sheets

E = Eᴿ = 0

(ii) Electric field at point in between the charged sheets

Eᴽ = σ/ε₀

Illustration: Find electric field intensity due to long uniformly charged wire. (charge per unit length is λ)

Solution:

Elemental charge dq = λ dℓ.

Field at point P is dE = K dq/R²

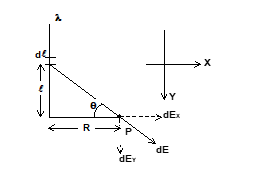
Then,

dEₓ = (λ dℓ cos θ)/(4πε₀R²)

on integration,

Eₓ = λ/(4πε₀R)

Also

dEᵧ = (λ dℓ sin θ)/(4πε₀R²)

On integration

Eᵧ = λ/(4πε₀R)

E = √(Eₓ² + Eᵧ²) = λ√2/(4πε₀R)

and

tan⁻¹(Eᵧ/Eₓ) = 45°

DIPOLE

Two equal and opposite charges separated by a small distance constitute an electric dipole

P⃗ = q × 2a⃗

P⃗ is directed from –ve to the +ve charge

(i) Electric field at an Axial Point

E = (1/4πε₀) × (2Px/[x² - a²]²)

For x >> a

E = (1/4πε₀) × (2P/x³)

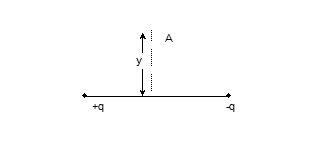
(ii) At a point on its perpendicular bisector

E = (1/4πε₀) × (P/[y² + a²]³/²)

For y >> a

E = (1/4πε₀) × (P/y³)

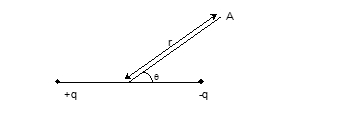
(iii) At any point

r >> a

E = (1/4πε₀) × (2P cos θ/r³)

E = (1/4πε₀) × (P sin θ/r³)

E = (1/4πε₀) × (P/r³) × √(1 + 3cos²θ)

Angle φ = tan⁻¹(1/2 tan θ)

GAUSS THEOREM

The flux of an electric field E⃗ through an arbitrary closed surface S is equal to the algebraic sum of the charge enclosed by this surface divided by ε₀.

∮ E⃗ · ds⃗ = qᵢₙ/ε₀

The Gauss theorem can be effectively applied to calculation of fields only when a field has special symmetry in most cases, plane, cylindrical or circular

Illustration: Figure shows a section of an infinite rod of charge having linear charge density λ which is constant for all points on the line. Find electric field E at a distance r from the line.

Solution:

From symmetry, E⃗ due to a uniform linear charge can only be radially directed. As a Gaussian surface, we can choose a circular cylinder of radius r and length l, closed at each end by plane caps normal to the axis.

The direction of E⃗ is radially outward for a line of positive charge.

Illustration: Figure shows a spherical symmetric distribution of charge of radius R. Find electric field E for points A and B which are lying outside and inside the charge distribution respectively.

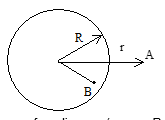
Solution:

The spherically symmetric distribution of charge means that the charge density at any point depends only on the distance of the point from the centre and not on the direction. Secondly, the object can not be a conductor, or else the excess charge will reside on its surface.

Now, apply Gauss's law to a spherical Gaussian surface of radius r (r > R for point A)

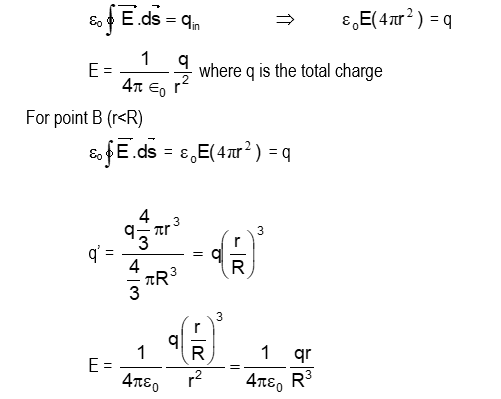
Electric Potential

Amount of work done in moving unit positive charge from infinity upto the point under consideration, against the field of a given charge q.

In other words, it is negative of the work done by the internal forces.

V = -∫∞ʳ E⃗ · dr⃗

= (1/4πε₀) × (q/r)

It is a scalar quantity. Its unit is volt.

(i) Potential at a point due to several charges

V = V₁ + V₂ + V₃ + …

(ii) Potential of a point due to an electric dipole

V = (1/4πε₀) × (P cos θ/(r² - a² cos²θ))

p = dipole moment

For r >> a

2a = length of dipole

V = (1/4πε₀) × (P cos θ/r²)

r = distance of a point from centre of dipole

Potential due to a uniformly charged disc

(i) At a point on its axis

V = (σ/2ε₀) × [√(x² + R²) - x]

Here σ = surface charge density on disc

(ii) At the centre of the disc

R = radius of disc

and x = distance of a point from centre of disc

V = (σR/2ε₀)

Potential at the edge of a uniformly charged disc

V = (σR/ε₀)

Potential at the apex of a cone having charge Q distributed uniformly on its curved surface and having slanting length L

V = (Q/2πε₀L)

Potential of a conducting sphere of radius R at a distance r from the centre

(i) r > R

V = Kq/r

q – charge on the sphere

(ii) r = R

V = Kq/R

K = 1/(4πε₀)

(iii) r < R

V = kq/R

Potential of a dielectric sphere

(i) if r > R

q – total charge in the dielectric sphere

V = Kq/r

(ii) if r = R

V = Kq/R

(iii) if r < R

V = Kq[3/(2R) - r²/(2R³)]

Dipole in a uniform electric field:

A dipole placed in a uniform electric field with angle θ between p⃗ and E⃗ (F⃗ ≠ 0)

• Stable equilibrium: When θ = 0°, F = τ = 0, U = minimum = -PE.
• Unstable equilibrium: When θ = 180°, F ≠ 0, τ = 0, U = max = PE

Work done in rotating the dipole from initial position θ₁ to θ₂

W = PE[cos θ₁ - cos θ₂]

Note:

1. When dipole placed in a non-uniform electric field, F⃗ ≠ 0.
2. A dipole P is placed in the field of a linear charge distribution.
   • a) Net force = 0, τ ≠ 0
   • b) Net force ≠ 0, τ ≠ 0

Illustration: Two conducting spheres having radii a and b charged to q₁ & q₂ respectively. Find the potential difference between 1 & 2?

Solution:

The potential on the surface of the sphere 1 is given by

v₁ = (1/4πε₀) × (q₁/a) + (1/4πε₀) × (q₂/b) .... (a)

The potential on the surface of the sphere 2 is given by,

v₂ = v₁ - v₂

Δv = (q₁/4πε₀) × [1/a - 1/b]

Electric Potential Energy

The electric potential energy of a system of point charges is the amount of work done in bringing the charges from infinity in order to form the system. For point charges q₁ and q₂ are separated at a distance r₁₂, Electric potential energy of the system q₁ and q₂

U = (1/4πε₀) × (q₁q₂/r₁₂)

For three particle system q₁, q₂ and q₃

U = (1/4πε₀) × [q₁q₂/r₁₂ + q₁q₃/r₁₃ + q₂q₃/`r₂₃]

We can define electric potential (Vₚ) at any point P in a electric field as , Vₚ = Uₚ/q₀; where Uₚ, is the change in electric potential energy in bringing the test charge q₀ from infinity to point P.

Illustration: Determine the interaction energy of the point charges of the following set-up

Solution:

U = U₁₂ + U₁₃ + U₁₄ + U₂₃ + U₂₄ + U₃₄

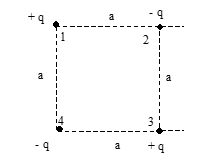
= -kq²/a + kq²/(a√2) - kq²/a + kq²/(a√2) - kq²/a + kq²/(a√2)

= -3kq²/a²

(Here k = 1/4πε₀)

Exercise 2.

• Derive is the electric field at any point on the axis of a charged rod of length `L' and linear charge density`λ'? The point is separated from the nearer end by a.

• A ring shaped conductor with radius R carries a total charge q uniformly distributed around it as shown in the figure. Derive Find the electric field at a point P that lies on the axis of the ring at a distance x from its centre.

• Two free particles (i.e. free to move) with charge +q and +4q are a distance L apart – A third charge is placed so that the entire system is in equilibrium.
  1. Find the location, magnitude and sign of third charge.
  2. Show that the equilibrium is unstable.
• What is the slope of equi-potential surfaces for
  1. infinite line of charge and
  2. point charge.

CAPACITORS

• Capacitance

If Q is the charge given to a conductor and V is the potential to which it is raised by this amount of charge, then it is found Q ∝ V. Or Q = CV, where C is a constant called capacitance of the conductor.

• Capacitor

A pair of conductors separated by some insulating medium is called a capacitor. This medium is called dielectric of the capacitor. If units of the charge is given to one of the conductors, and thereby a potential, difference V is set up between the conductors, the capacitance is then defined as

C = Q/V

For parallel plate capacitor

C = ε₀εᵣA/d

i.e. the capacitance does indeed, depends only on geometrical factors namely, the plate area and plate separation.

• Spherical Capacitor

C = (1/4πε₀) × (R₁R₂/(R₂ - R₁))

• Isolated Capacitor

An isolated sphere can be thought of as a capacitor where other plate is at infinity.

R₁ = R

R₂ = ∞

C = 4πε₀R₁ = 4πε₀R/1

• Cylindrical Capacitor

C = 2πε₀/ln(R₂/R₁)

Combination of Capacitors

• Series Combination:

In series combination, each capacitors has equal charge for any value of capacitance. Equivalent capacitance C is given by

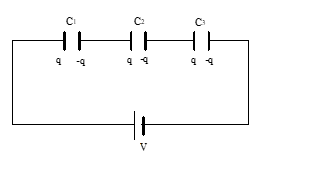
1/C = 1/C₁ + 1/C₂ + 1/C₃

• Parallel Combination:

In parallel combination the potential differences of the capacitor connected in parallel are equal for any of capacitor. Equivalent capacitance is given by

C = C₁ + C₂ + C₃

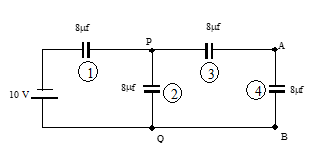
Illustration: In the above circuit, find the potential difference across AB.

Solution:

Let us mark the capacitors as 1,2,3 and 4 for identifications. As is clear, 3 and 4 are in series, and they are in parallel with 2. The 2,3,4 combine is in series with 1.

C₃₄ = (C₃ × C₄)/(C₃ + C₄) = 4μF

C₂,₃₄ = C₂ + C₃₄ = 12μF

Ceq = (C₁ × C₂,₃₄)/(C₁ + C₂,₃₄) = 4.8μF

q = CeqV = 48μC, V₁=q/c=6v

VPQ = 10 - 6 = 4V

By symmetry of 3 and 4, we say, VAB = 2V.

Dielectric

Substances having polar atoms/molecules intrinsically or being polarized are called dielectrics.

Non-Polar Dielectric

Substances which do not have polar atoms/molecules intrinsically but get polarized parallel to the external applied electric field.

Polar Dielectric

Substances which have polar atoms/molecules intrinsically but are randomly arranged. On application of external electric field they get polarized parallel to the external electric field.

Net electric field inside dielectric.

E = E₀ - E₁

E = E₀(1 - 1/K)

σ – surface charge density of capacity plates

σ' = σ(1 - 1/K)

σ' – bound charge density

σ' = σ(1 - 1/K)

Capacitance of a parallel plate capacitor having dielectric slabs in series.

C = ε₀A/[t₁/K₁ + t₂/K₂]

Energy stored in a Capacitor

UC = Q²/(2C) = (1/2)CV² = (1/2)Q·V

Energy supplied by Source

US = Q. V.

Energy lost in form of heat

= (1/2)Q.V

Energy density of the electric field

u = (1/2)ε₀E²

in free space

u = (1/2)Kε₀E²

in presence of dielectric medium ; K - dielectric const.

Force on a Dielectric in a Capacitor

F = (Q²/2C²) × (dC/dx)

when source is connected

V = Q/C

F = (1/2)V² × (dc/dx)

Illustration: A 4μf capacitor is charged to 150 V and another 6μf capacitor is charged to 200 V. Then they are connected across each other. Find the potential difference across them. Calculate the heat produced.

Solution:

4μf charged to 150 V would have q₁ = C₁V₁ = 600μC

6μf charged to 200 V would have q₂ = C₂V₂ = 1200μC

After connecting them across each other, they will have a common potential difference V.

Charges will readjust as q₁' and q₂'

Initial energy = (1/2)C₁V₁² + (1/2)C₂V₂² = (1/2)(4μF)(150V)² + (1/2)(6μF)(200V)² = 0.165J

[conservation of charge] q₁' + q₂' = q₁ + q₂ = 1800μC

C₁ + C₂ = (4 + 6)μF = 10μF

V = 1800μC/10μF = 180 volt

Final energy

Uf = (1/2)(C₁ + C₂).V² = (1/2)(4μF + 6μF)(180)² = 0.161J

Heat produced = |Uf - Ui| = 0.003 J

Exercise 3:

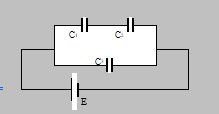
• Three capacitors are connected as shown in the figure, where
  C₁ = 3μF, C₂ = 6μF, C₃ = 2μF
  And E = 10 Volt. Find the energy drawn from the source.

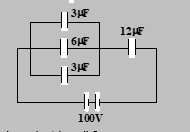
• Find the potential difference across the capacitor of 12μF.

• What is the basic difference between charged capacitor and an electric cell?

ANSWERS TO EXERCISES

Exercise 1

1. Yes, along equipotential surface.
2. q = Q/2
3. No

Exercise 2

3. -4q/9 at a distance L/3 from q.
4. a) Cylindrical b) Spherical

FORMULAE AND CONCEPTS AT A GLANCE

1. Charge is quantized i.e, q = ne⁻, where n = 1,2,3 …….. and e = 1.6 x 10⁻¹⁹ C
2. Coulomb's Law, Fe = (1/4πε₀) × (q₁q₂/r²)
3. Electric field , E = (1/4πε₀) × (q/r²)
4. Electric potential , V = (1/4πε₀) × (q/r)
5. E = -dV/dr
6. In Parallel plate capacitor, capacitance = C = ε₀A/d ; d = distance between plates and A = area of cross section of plate
7. Energy stored in capacitor = (1/2)(q²/C) = (1/2)CV² = (1/2)qV

SOLVED PROBLEMS

Problem 1: Four charges equal to –Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium, the value of q is.

Options:

(A) -Q(1 + 2√2)/4 (B) -Q(1 - 2√2)/4 (C) -Q(1 + 2√2)/2 (D) -Q(1 - 2√2)/2

Solution:

Consider the equilibrium of any charge – Q

(1/4πε₀) × (2Q²/a²) × (1/√2) = (1/4πε₀) × (Qq/(a/√2)²)

q = -Q(1 - 2√2)/4

Answer: (B)

Problem 2: Potential in the x-y plane is given as V = 5(x² + xy) volts. The electric field at the point (1, -2) will be

Options:

(A) 3ĵ V/m (B) -5ĵ V/m (C) 5ĵ V/m (D) -3ĵ V/m

Solution:

Ex = -∂V/∂x = -(10x + 5y) = -10 + 10 = 0

Ey = -∂V/∂y = -5x = -5

E⃗ = -5ĵ V/m

Answer: (B)

Problem 3: The equivalent capacitance between points A and C of the circuit will be

Options:

(A) 12C (B) 6C (C) 3C (D) 24C

Solution:

Equivalent circuit of the above figure can be drawn as

CAB = 3C

Answer: (C)

Problem 4: Electric field in a region is given by E⃗ = 2(î + 3ĵ + 4k̂) V/m. The potential difference between points (0, 0, 0) and (1,2,3) will be

Options:

(A) 2 V (B) 5 V (C) 4V (D) 6 V

Solution:

p.d. across the points = -∫ E⃗ · dr⃗

V₂ – V₁ = -2(î + 3ĵ + 4k̂) · (î + 2ĵ + 3k̂)

= -2 - 6 + 12 = 4 volts.

Answer: (C)

Problem 5: What is the mechanical work done in pulling the slab out of the capacitor after disconnecting it from the battery

Options:

(A) (1/2)E²C(εᵣ-1) (B) E²C (C) E²C(εᵣ - 1) (D) none of these

Solution:

Work done = change in potential energy

= U₂ – U₁

v₁ = (1/2) E²C

v₂ = (1/2) E²C'/εᵣ = (1/2) E²Cεᵣ

Work done = (1/2) E²C (εᵣ – 1).

Answer: (A).

Problem 6: Two point charges each of charge +q are fixed at (+a, 0) and (-a, 0). Another positive point charge q placed at the origin is free to move along x- axis. The charge q at origin in equilibrium will have

Options:

(A) maximum force and minimum potential energy.

(B) minimum force & maximum potential energy.

(C) maximum force & maximum potential energy.

(D) minimum force & minimum potential energy.

Solution:

The net force on q at origin is

F⃗ = F⃗₁ + F⃗₂ = 0î

The P.E. of the charge q in between the extreme charges at a distance x from the origin along +ve x axis is

U = (1/4πε₀) × [q²/(a-x) + q²/(a+x)]

For U to be minimum, dU/dx = 0, d²U/dx² > 0

(a-x)² = (a + x)² ⟹ a + x = ±(a – x)

x = 0, because other solution is irrelevent.

Thus the charged particle at the origin will have minimum force and minimum P.E.

Answer: (D).

Problem 7: The capacitance of the system of parallel plate capacitor shown in the figure is

Options:

(A) ε₀A₁A₂/(d(A₂ + A₁)) (B) ε₀A₁A₂/(d(A₂ - A₁)) (C) ε₀A₁/d (D) ε₀A₂/d

Solution:

Since the electric field between the parallel charge plates is uniform and independent of the distance, neglecting the edge effect, the effective area of the plate of area A₂ is A₁. Thus the capacitance between the plates is

C = ε₀A₁/d

Answer: (C)

Problem 8: Two spherical conductors B and C having equal radii and carrying equal charges in them repel each other with a force F when kept apart at some distance. A third spherical conductor having same radius as that of B, but uncharged is brought in contact with B, then brought in contact with C and finally removed away from both. The new force of repulsion between B and C is

Options:

(A) F/4 (B) 3F/4 (C) F/8 (D) 3F/8

Solution:

We have F = (1/4πε₀) × (q²/d²)

When a (which is of same size as that of B) is brought in contact with B the charge on both becomes q/2.

When A, now containing a charge q/2 is brought in contact with c, charge on each becomes (q/2 + q)/2 = 3q/4

The new force of repulsion between B and C = (1/4πε₀) × (q/2 × 3q/4)/d² = 3F/8

Answer: D

Problem 9: The capacitance of an filled parallel plate capacitor is 20μF. The separation between the plates is doubled and the space between the plates is then filled with wax giving the capacitance a new value of 40×10¹² farads. The dielectric constant of wax is

Options:

(A) 12.0 (B) 10.0 (C) 8.0 (D) 4.2

Solution:

10×10¹² = ε₀A/d, 40×10¹² = Kε₀A/(2d)

K = 8

Answer: (C)

Problem 10: An electric dipole is placed at an angle of 30° with an electric field of intensity 2 x 10⁵ N/C. It experiences a torque equal to 4Nm. Calculate the charge on the dipole if the dipole length is 2cm

Options:

(A) 2mC (B) 4mC (C) 2mC (D) 4mC

Solution:

Torque τ = P⃗ × E⃗ = PEsinθ

Or, 4 = P × 2 × 10⁵ × sin30°

Or, P = 4/(10⁵ × 1/2) = 4 × 10⁻⁵ N.m.

Dipole moment, P = ql

Or, q = P/l = (4 × 10⁻⁵)/(2 × 10⁻³) = 2mC

Answer: A

ASSIGNMENT Questions

1. A cylinder of radius r and length ℓ is placed in a uniform electric field E parallel to the axis of the cylinder. Total electric flux through the surface of the cylinder is

   1. 2πrE
   2. πr²E
   3. (2πr + πr²)E
   4. Zero

2. Electric field due to a uniformly charged infinite non-conducting sheet having surface density σ is E. Electric field due to an infinite conducting sheet of the same surface charge density is

   1. E/2
   2. E
   3. 2E
   4. 4E

3. The potential on the surface of a spherical conductor of radius 3 m is 6 V. The potential at the centre is

   1. Zero
   2. 2 V
   3. 6 V
   4. 18 V

4. An electron moves with a velocity u in a uniform electric field ⃗E. If the angle between u and ⃗E is neither 0 nor π, the path followed by the electron is:

   1. Straight line
   2. Circle
   3. Ellipse
   4. Parabola

5. The potential difference reduces to 1/8 of original value for a 5 µF isolated parallel-plate charged capacitor when a glass plate is placed between plates. The value of relative dielectric constant of glass is

   1. 1.6
   2. 5
   3. 8
   4. 40

6. After charging, a parallel-plate capacitor is immersed in an oil of dielectric constant 2. The field between the plates is:

   1. Increased proportional to 2
   2. Decreased proportional to 1/2
   3. Increased proportional to √2
   4. Decreased proportional to 1/√2

7. Three charges 4q, Q and q are placed in a straight line of length ℓ at points 0, ℓ/2, ℓ respectively. What should be Q so as to make the force on q zero?

   1. −q/2
   2. −q
   3. −2q
   4. −4q

8. Three small spheres each carrying a charge q are placed on the circumference of a circle of radius R, forming an equilateral triangle. If we place another charge Q at the center of the circle, the force on Q is

   1. Zero
   2. qQ/(4πε₀R²)
   3. qQ/(4πε₀R²√2)
   4. qQ√3/(4πε₀R²)

9. Two small spheres each carrying a charge q are placed 1 m apart. The electric force between them is F Newton. If one sphere is taken around the other, the work done by F in one revolution is

   1. F Joule
   2. 2F Joule
   3. F/2 Joule
   4. Zero

10. A point body of mass 2 g and charge 2 µC, on being released from rest, moves through a potential difference of 1000 V. What will be the velocity acquired by the body?

    1. 2 m/s
    2. √2 m/s
    3. 1/√2 m/s
    4. 1/2 m/s

11. A thin spherical shell of radius R carries a uniform surface charge density σ. The electric field inside the shell is

    1. Zero
    2. σ/ε₀
    3. σ/(2ε₀)
    4. σR/ε₀

12. The equivalent capacitance between A and B when two capacitors C₁ and C₂ are connected in parallel is

    1. C₁ + C₂
    2. (C₁C₂)/(C₁ + C₂)
    3. C₁ − C₂
    4. 1/(C₁ + C₂)

13. The potential at a point due to a point charge q at distance r is given by

    1. q/r²
    2. q/(4πε₀r²)
    3. q/(4πε₀r)
    4. 4πε₀q/r

14. The energy stored in a capacitor of capacitance C charged to a potential difference V is

    1. CV
    2. ½CV²
    3. 2CV²
    4. V²/(2C)

15. The SI unit of permittivity of free space (ε₀) is

    1. C²/N·m²
    2. N·m²/C²
    3. C/N·m²
    4. N/C²

ANSWERS TO ASSIGNMENT

1.	2.	3.	4.	5.
D	C	C	D	C
6.	7.	8.	9.	10.
B	B	A	D	B
11.	12.	13.	14.	15.
D	D	B	C	B