Modern Physics

Understanding Modern Physics: From Atomic Structure to Nuclear Phenomena

Modern physics represents a revolutionary departure from classical physics, fundamentally changing our understanding of matter, energy, and the universe at the atomic and subatomic scale. This comprehensive exploration covers the essential concepts that form the foundation of quantum mechanics and nuclear science.

The Evolution of Atomic Models

Rutherford's Nuclear Model

Ernest Rutherford's groundbreaking gold foil experiment in the early 20th century revealed the nuclear structure of atoms. By bombarding a thin gold foil with high-energy α-particles, Rutherford observed that most particles passed through undeflected, while a small fraction were scattered at large angles. This led to his revolutionary conclusion that atoms consist of a tiny, dense, positively charged nucleus surrounded by mostly empty space where electrons orbit.

The experimental observations demonstrated that the nucleus contains virtually all of an atom's mass concentrated in an incredibly small volume, with the nuclear radius being approximately 10,000 times smaller than the atomic radius. This discovery laid the groundwork for our modern understanding of atomic structure.

Bohr's Quantum Atomic Model

Niels Bohr addressed the limitations of Rutherford's model by introducing quantum concepts. Classical physics predicted that orbiting electrons should continuously radiate energy and spiral into the nucleus, making atoms unstable. Bohr's model introduced revolutionary postulates:

Quantized Angular Momentum: Electrons can only orbit in specific "allowed" orbits where their angular momentum equals an integer multiple of ℏ (h/2π). This quantization condition is expressed as mvr = nℏ, where n is the principal quantum number.

Stationary States: Electrons in these allowed orbits do not radiate energy, maintaining constant energy levels. Energy is only absorbed or emitted when electrons transition between these discrete energy levels.

Energy Level Transitions: When an electron transitions from a higher energy level (n₂) to a lower one (n₁), it emits a photon with energy equal to the difference between the levels: ΔE = E₂ - E₁ = hf.

Wave-Particle Duality and de Broglie Waves

Louis de Broglie's revolutionary proposal in 1924 suggested that all matter exhibits wave-like properties. The de Broglie wavelength λ = h/p associates a wavelength with any particle having momentum p. This concept was experimentally verified through electron diffraction experiments by Davisson and Germer, confirming that electrons can indeed behave as waves.

For electrons accelerated through a potential difference V, the de Broglie wavelength becomes λ = h/√(2m_eV), where m_e is the electron mass. This wave nature of matter is fundamental to quantum mechanics and explains phenomena such as electron orbitals in atoms.

The Photoelectric Effect and Quantum Nature of Light

Einstein's explanation of the photoelectric effect earned him the Nobel Prize and established the quantum nature of light. When electromagnetic radiation strikes a metal surface, electrons are ejected if the photon energy exceeds the material's work function (φ).

The maximum kinetic energy of photoelectrons follows Einstein's photoelectric equation: KE_max = hf - φ, where f is the photon frequency. This relationship demonstrates that electron kinetic energy depends on frequency, not intensity, supporting the particle nature of light through discrete energy packets called photons.

The stopping potential V_s required to halt the most energetic photoelectrons is related to the maximum kinetic energy by eV_s = KE_max, providing a direct method to measure Planck's constant and work functions.

X-Ray Production and Characteristics

X-rays are produced when high-energy electrons strike a target material in devices like Coolidge tubes. Two types of X-ray spectra result:

Continuous X-rays: Generated when electrons lose kinetic energy through multiple collisions, producing a continuous spectrum with a minimum wavelength λ_min = hc/eV, where V is the accelerating voltage.

Characteristic X-rays: Produced when incident electrons knock out inner shell electrons, creating vacancies that are filled by electrons from higher energy levels. The resulting X-rays have wavelengths characteristic of the target material.

Moseley's law, √f = a(Z - b), relates X-ray frequency to atomic number Z, providing crucial evidence for atomic structure and enabling determination of atomic numbers.

Nuclear Physics and Radioactivity

Nuclear physics explores the properties and behavior of atomic nuclei. Key concepts include:

Mass-Energy Equivalence: The binding energy of a nucleus equals the mass defect multiplied by c²: BE = Δmc². This energy represents the work required to separate all nucleons.

Radioactive Decay: Unstable nuclei undergo spontaneous decay following the exponential law N(t) = N₀e^-λt, where λ is the decay constant. The half-life T₁/₂ = ln(2)/λ represents the time for half the nuclei to decay.

Nuclear Reactions: Processes like fission and fusion release enormous energy due to the conversion of mass to energy, forming the basis for nuclear power and stellar energy production.

Essential Modern Physics Formulas

Formula Name	Mathematical Expression	Description
de Broglie Wavelength	λ = h/p = h/mv	Wavelength associated with matter waves
Electron de Broglie (Accelerated)	λ = h/√(2meV)	Wavelength for electron through potential V
Bohr Angular Momentum	L = mvr = nℏ	Quantized angular momentum condition
Bohr Energy Levels	En = -13.6Z²/n² eV	Energy of electron in hydrogen-like atoms
Bohr Radius	rn = n²ℏ²/(meke²Z)	Orbital radius in Bohr model
Photoelectric Effect	KEmax = hf - φ	Maximum kinetic energy of photoelectrons
Stopping Potential	eVs = hf - φ	Potential to stop photoelectrons
X-ray Minimum Wavelength	λmin = hc/eV	Shortest wavelength in continuous spectrum
Moseley's Law	√f = a(Z - b)	X-ray frequency vs atomic number
Radioactive Decay	N(t) = N₀e-λt	Exponential decay law
Half-life	T₁/₂ = ln(2)/λ = 0.693/λ	Time for half of nuclei to decay
Binding Energy	BE = Δmc²	Nuclear binding energy from mass defect
Mass Defect	Δm = Zmp + (A-Z)mn - mnucleus	Difference in mass of separated nucleons

These fundamental concepts and relationships form the cornerstone of modern physics, enabling our understanding of atomic behavior, quantum phenomena, and nuclear processes that govern the universe from the smallest scales to stellar interiors.

Atoms

Matter is composed of small particles called molecules which can be further subdivided into atoms. Until the end of the 19th century it was believed that atoms were indivisible but later it was found that atoms were composed of smaller subatomic particles - electrons, protons and neutrons.

Electrons are light negatively charged particles, protons are heavy positively charged particles while neutrons are heavy neutral particles. The exact structure of the atom and the forces responsible for holding these particles together were the subject of investigation in those times.

Several models were proposed to explain atomic structure: the Thomson model, the Rutherford model, the Bohr model and so on. In this section we are going to study the Rutherford and Bohr models of the atom.

Rutherford's Model

Experiment: Rutherford bombarded a high energetic α-particles on a thin Gold foil. Observations: He observed that:

1. Most of the α-particles passed undeviated.
2. Few α-particles passed with very small deviation.
3. A very few α-particles got deviated through large angles, one in a million of α-particles (got deviated through 180°) retraced its path.

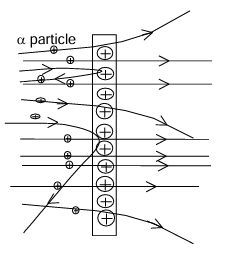
Conclusions: He concluded that:

1. Since most of the α-particles passed undeviated through the gold foil, the majority of the space occupied by the matter is vacuum (empty). Maximum part of an atom is empty space.
2. Since few α-particles get deviated through small angles, there must be some positively charged particles in matter which repel the α-particles causing such deviation. He named these heavy positively charged particles as "nucleus". Center of an atom is a positively charged nucleus.
3. As, very few α-particles got deviated through large angles & retraced their path, the size of the nucleus is very small compared to an "atom". Center of an atom is a massive nucleus.

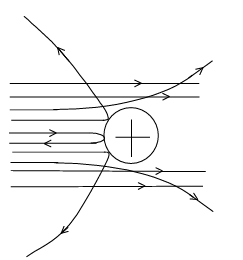
Suggested Model

(a) Electrons (pre-conceived negatively charged particles having negligible mass) revolve around a fixed positively charged centre in different orbits, just like the planets revolve around the sun. The electrostatic attraction (Coulombic force) between an electron & nucleus provides the necessary centripetal acceleration. Consequently, the electrons can move in the orbits. (b) The orbits of revolution of the electrons are circular.

Limitations

By that time it was known that when a charged particle accelerates, it emits electromagnetic radiation. That means, an accelerating (oscillating) charge must radiate (lose) energy. If this principle is to be held good, an electron moving in a circular path experiencing centripetal acceleration must have to lose energy.

Consequently its kinetic energy will decrease, therefore its speed will decrease at any position where as the force of attraction between the electron & nucleus remains unchanged. As a result the electron can not have a stable circular orbit. As it continuously loses energy (speed), it will at last collapse into the nucleus but this does not happen in practice (nature).

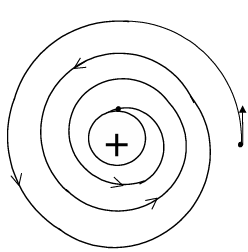
Then this limitation was analysed carefully by Neils Bohr, a renowned physicist. He tried to overcome the limitation arisen in Rutherford's model & gave a more satisfactory model to explain the possible structure of a simplest atom, that is hydrogen. This is known as Bohr's atomic model.

De-BROGLIE Waves

In 1925, de Broglie proposed that the wavelength (λ) of waves associated with particles of momentum 'p' is given by λ = h/p = h/(mv) This was later verified by the experimental results of Davisson and Germer on electron diffraction. It is assumed that the voltage V is not more than several tens of kV). The wavelength associated with an electron accelerated through a potential difference of V volt is given by λ = h/√(2eVmₑ) (It is assumed that the voltage V is not more than several tens of kV)

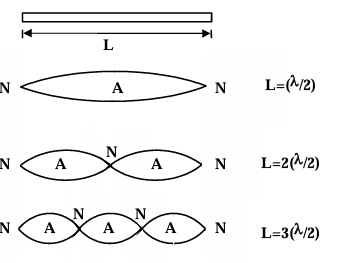
Example: A particle of mass m is confined to a narrow tube of length L. Find

1. the wavelengths of the de-Broglie wave which will resonate in the tube,
2. the corresponding particle momenta, and
3. the corresponding energies.

Solution: (a) The de Broglie waves will resonate with a node at each end of the tube.

A few of the possible resonance forms are as follows: λₙ = 2L/n ; n = 1, 2, 3, ......

(b) Since de-Broglie wavelengths are λₙ = h/pₙ ∴ pₙ = h/λₙ = nh/(2L) n = 1, 2, 3....

(c) (KE)ₙ = pₙ²/(2m) = n²h²/(8L²m), n = 1, 2, 3, ........

Example:  What is the energy and wavelength of a thermal neutron at a temperature of 20° C.

Solution: By definition, a thermal neutron is a free neutron in a neutron gas at about 20° C (293 K).

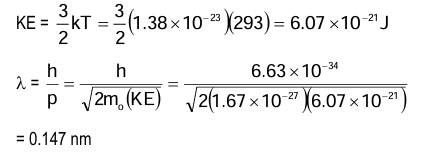
KE = (3/2)kT

= (3/2)(1.38 × 10⁻²³)(293)

= 6.07 × 10⁻²¹ J λ = h/p

= h/√(2mₙ(KE)) = (6.63 × 10⁻³⁴)/√(2(1.67 × 10⁻²⁷)(6.07 × 10⁻²¹))

= 0.147 nm

BOHR'S Atomic Model

(i) Bohr introduced the concept of "radiationless circular" orbits to overcome the difficulty of radiation of energy by accelerating electron in an atom. He postulated that, the electron moves around the fixed nucleus in some fixed circular paths in which neither it radiates (loses) energy nor it gains energy.

These are known as radiationless orbit or fixed circular orbit. Therefore, the energy of an electron in a particular orbit remains constant. He numbered these circular orbits as n (1, 2, 3 etc. ). These are known as principal quantum numbers. The electron can not move in a circular path other than these orbits. The energy of an electron in a particular orbit remains constant. When an electron absorbs energy, it jumps from a lower energy level n₁ to higher energy level n₂ (n₂ > n₁). This is known as excitation.

Similarly when an electron loses (radiates) energy it jumps from higher to lower energy level. This is known as de-excitation. The difference of energy between any two energy levels (fixed orbits) = energy lost (radiated)/energy gained ΔE = nhf = nhc/λ Where n = numbers of photons emitted or absorbed by the electron, f & λ are the frequency & wavelength of radiation.

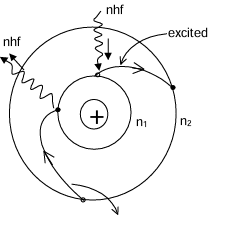
An electron remains excited/de-excited for a very short time in the order of 10⁻⁶ s between any two fixed/stationary/radiationless orbits. During this time it does not experience pure circular motion between two stationary orbits. This transient unstable phase is known as transition & the time of excitation or de-excitation is known as transitional period.

(ii) After, his brilliant postulation of radiationless orbit (constant energy levels) or quantisation of energy of an electron/orbit, N. Bohr quantised the angular momentum of the orbit. He argued that if the speed/energy of an electron is quantised, the radius of the orbit is also quantised (fixed).

That means an electron can not move in the circular orbits of any arbitrary radius. If the speed (v) & radius (r) for an orbit remain constant (quantised), then according to the classical mechanics the angular momentum (mvr) must have to be a constant quantity for an orbit. In the other words, we can say that the angular momentum of an electron is quantised. L = mvr = nh/(2π) where n = 1, 2, 3…… (n = principal quantum numbers) Angular momentum of an electron in an orbit is integral multiple of h/(2π).

Where h = Planck's constant = 6.63 × 10⁻³⁴ Js. Using the concepts of classical mechanics & classical electrodynamics we will develop the expressions for radius, orbital speed, potential energy, kinetic energy, total energy, frequency of revolution etc. in terms of the electronic mass m, electronic charge e, planck's constant h etc.

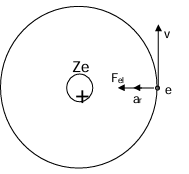
Radius

Electron experiences a centripetal force, that is the electrostatic force of attraction Fₑₗ between the nucleus of charge Ze,

where Z = atomic number. Fₑₗ = maᵣ = mv²/r = rω²

According to Coulomb's Law: Fₑₗ = (1/4πε₀) × (Ze²/r²) mv²/r

= Ze²/(4πε₀r²)

v² = Ze²/(4πε₀rm) Eliminating v by using the expression mvr = nh/(2π)

We obtain, Ze²/(4πε₀rm)

= (nh/2πmr)² r

= (ε₀n²h²)/(πZme²) Since ε₀, h, Z, m etc. are constants for all orbits (except n & Z), we express r in terms of n and Z as r = (r₀n²)/Z where r₀ = (ε₀h²)/(πme²) is known as the radius of the orbit of an electron in its ground state n = 1, of a hydrogen atom (z = 1) Numerically, r₀ = 0.53 Å.

Hence r(n) = 0.53 (n²/Z)Å.

Orbital Speed

mvr = nh/(2π) v = nh/(2πrm) putting the obtained value of r we get v = nh/(2πm) × (πZme²)/(ε₀n²h²) V = Ze²/(2nε₀h) ⇒ v = v₀Z/n where v₀= e²/(2ε₀h) is the speed of an electron in Bohr's ground state orbit of hydrogen atom.

Angular velocity and frequency of revolution

ω = v/r = (Ze²/2nε₀h) × (πZme²/ε₀n²h²) = πmZ²e⁴/(2ε₀²h³n³) & frot = πmZ²e⁴/(4ε₀²h³n³)

Energy of the electron

In any orbit electron possesses two types force energy, electric potential energy and kinetic energy. P.E. = -(1/4πε₀) × (Ze)e/r(n) . . . (1) K.E. = (1/2)mv² Also, mv²/r = (1/4πε₀) × (Ze)e/r²(n) Now total energy Eₙ = P.E. + K.E. E(n) = -(1/4πε₀) × Ze²/rₙ + (1/2) × (1/4πε₀) × Ze²/rₙ = -(1/8πε₀) × Ze²/rₙ Putting the value of r(n), we get Eₙ = -Z²e⁴m/(8ε₀²h²n²)

Energy of the electron in the ground state of hydrogen atom

For hydrogen atom Z = 1 and for ground state n = 1 E₁(H, atom) = -e⁴m/(8ε₀²h²) = -13.6 eV. Energy of the electron in the nth orbit of hydrogen atom can be given by the expression Eₙ = E₁/n² = -13.6/n² Energy of the electron in the nth orbit of hydrogen like atom with atomic number Z can be given by the expression. Eₙ = -13.6Z²/n²

Origin of Spectra

So long an electron revolves around the nucleus in a particular orbit, its energy remains constant. When electron gets energy, it suddenly jumps into higher energy level. Since electron can not stay in excited state forever, hence it jumps into lower energy level to achieve the stability. Subsequently energy is radiated in the form of photons. "The transition of electron of one orbit to the other orbit is the origin of spectra."

The energy of the photon is equal to the difference of the energies of the two orbits. i.e. E = -13.6 z² [(1/(nf)²) - (1/(ni)²)] eV Here Z = atomic number ni = principal quantum number of initial orbit. nf = principal quantum number of final orbit. The above expression is valid only for hydrogen or hydrogen like atom.

Example: Find the orbital magnetic dipole moment of the electron in hydrogen atom.

Solution: The orbiting electron behaves as a current loop.

The equivalent current i = net charge/time of revolution = e/T = efrot Now, magnetic dipole moment μ = niA

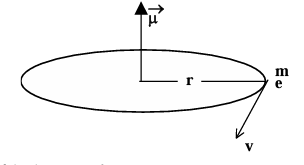
n = number of the turns of the loop = 1,

A = area of the loop = πr² μ =(1) (efrot) (πr²) 

μ = eπr²frot Putting the values of frot and r we obtain, μ = e × (ε₀n²h²/πme²Z²) × (πmZ²e⁴/4ε₀²h³n³)

= ehn/(4πm)

Photoelectric Effect

It was Sir Isaac Newton who gave the corpuscular theory of light. The greatest scientist Einstein supported this theory strongly on the basis of his experimental fact. While Einstein was working on the particle nature of light, he observed in his experiment that when light of sufficiently low wave length falls on a metal surface electrons are ejected. This phenomenon is known as "photoelectric effect." The ejected electrons are known as 'photo electrons'. The particles of light are called photons. Following are the properties of photons.

1. It carries momentum which is given by the expression P = h/λ, where h = planck's constant and λ = wavelength of the light
2. It carries energy, which is given by the expression E=hν, where ν = frequency of light = c/λ

Question arises: Does photon have mass as it carries momentum? Photon behaves like a particle, as it imparts momentum. It can not be in the state of rest. When it is brought to rest, it gets converted into energy, which equal to hν = hc/λ. Because of this fact it is called that rest mass of the photon is zero.

3. If intensity of light is increased keeping frequency constant, number of photons increases. Intensity of light can also be increased by increasing frequency.
4. When photon collides with a material particle, the total momentum and net energy remains constant. Photon may be absorbed or new photon can be emitted during collision.

Photoelectrons

It is found that number of photoelectrons is not exactly equal to the number of photons hitting the surface. Also energy (K.E.) of ejected electron is not equal to the energy of the photon. In fact when photon collides with the free electron, it transfers its momentum and energy to the electron. Electron comes out of the metal or not, it depends on where it is located.

The electron which is just on the surface of the metal requires less energy than to that which is inside the metal to come out. The minimum energy needed to eject the electron from the surface of the metal is known as work function of the metal. For different metals work function is different.

The photon having energy at least equal to the work function can eject the electron. Frequency of the photon whose energy is just equal to work function is called threshold frequency. Electron will come out of the surface if frequency of the photon will be greater than threshold frequency.

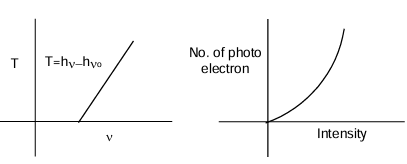
Kinetic energy of photoelectron

Different photo electrons have different kinetic energies. Suppose energy of the incident photon is E and work function of the metal is w then the maximum K.E. that the photo electron can have is given by the expression T = E – w If frequency of the photon is ν and threshold frequency for the metal is ν₀, then T = h(ν – ν₀) Since T can not be negative hence for ν < ν₀, electron can not be ejected. We can draw two conclusions:

1. The kinetic energy of the ejected electron depends on the frequency of the photon.
2. The number of ejected electrons depends the intensity of the light if frequency is constant.

Stopping Potential

If polarity of the battery is reversed and then gradually its potential increases the photo current will start decreasing. At certain potential the most energetic electron will also be not able to reach. This potential is known as stopping potential. If vs be the stopping potential then eVs = hν - w ∴ Vs = hν/e - w/e Vs = hν/e - φ where φ = (w/e) = work function (in electron volt)

X-RAYS

Production

1. It is also known as inverse photoelectric effect, as energetic electrons produce electromagnetic radiations.
2. Their wavelength is of the order of 1 Å.
3. They are produced with an apparatus called Coolidge tube.

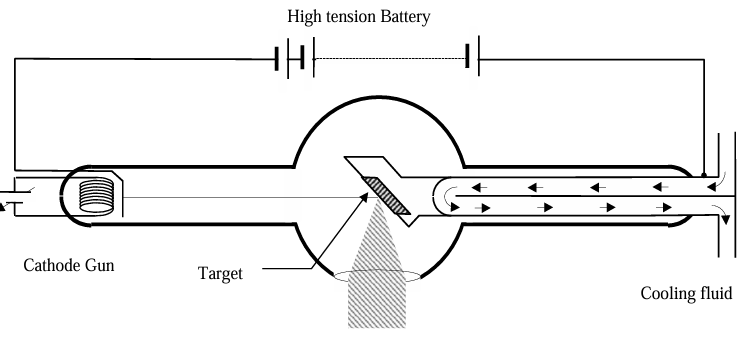
In a Coolidge tube, electrons are emitted by thermionic emission, accelerated across a very high potential difference V and made to hit a target. X-rays are produced and emerge out of a window. Water is circulated in the target to keep it cool

Continuous and Characteristic X-Rays

1. When an accelerated electron hits the target, the electron loses its energy in two process. One process gives rise to continuous X-rays and the other process gives rise to characteristic X-rays.
2. When the electron loses its kinetic energy in several collisions with the atoms, a fraction of the lost kinetic energy is converted into electromagnetic radiations. This fraction can range from zero to one.
3. Corresponding to the maximum kinetic energy lost by an electron, we have the largest frequency of the X-ray or the shortest wavelength. Kmax = eV = hc/λmin ∴ λmin = hc/eV. The emitted wavelengths range from a minimum value all the way to infinity. Thus the name continuous spectrum.
4. The other possibility is that the accelerated electron might knock out the inner electron of the target atom, whereby a vacancy is created in the inner orbit. Electrons from the higher orbit jump in to fill this vacancy, while releasing the energy difference as electromagnetic radiations.
5. These wavelengths are characteristic of the material from which they are emitted. Hence the name Characteristic Spectra.

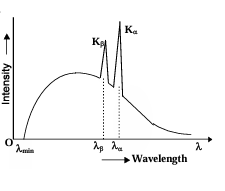
Moseley's Law

Moseley gave an empirical law. √f = a(Z - b) f = frequency of X-ray, Z = atomic number of target atom, a, b are constants.

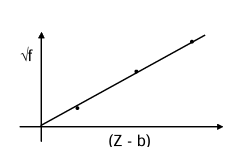
It was proposed before to Bohr's theory, and we see that it agrees with the Bohr's model. For Kα-line, the L-electron jumps to a vacancy in the K-level. So for the L electron, there are Z protons in the nucleus and an electron in the K-shell which screens of the positive charge.

So the net charge the L electron experiences can be taken as (Z - 1)e.

Now, E = Rhc(Z - 1)² [(1/1²) - (1/2²)] hf = Rhc(Z - 1)² × (3/4)

f = (3/4)R.c (Z - 1)² If we compare the above with Moseley's formula, we see that for Kα line, a = √(3Rc/4) and b = 1.

Properties of X-Rays

1. X-rays do not get deflected by electric or magnetic fields.
2. When passed through gases, they produce ionisation.
3. X-rays diffraction is used to study crystal structures.
4. They have high penetrating power and are used in radiographs.

Nuclear Physics

Nucleus is a positively charged particle situated at the centre of the atom. Most of the mass of the atom is concentrated in the nucleus. Nucleus consists mainly of two types of particles, proton and neutron. Collectively these two particles are known as nucleons. Now we are going to define some terms.

1. Atomic Number: It is the number of protons present in the nucleus. Atomic number of any atom does not depend on the number of electron in it.
2. Mass Number: Total number of protons and neutrons is called mass number.

If atomic number of an atom is Z, number of neutrons present in the nucleus of the atom is N, then its mass number can be given by the expression, A = Z + N, where A = mass number. Depending on the number of protons and neutrons in the nucleus, all nuclei are categorised in three types.

1. Isotopes: Nuclei having same atomic number but different mass number are called isotopes. Ex. – ₁H², ₁H³
2. Isobars: Nuclei having same mass number but different atomic number are called isobars. Ex. – ₆C¹⁴, ₇N¹⁴
3. Isotones: Nuclei having same number of neutrons, but different atomic number and mass number are called isotones. Ex – ₁H³, ₂He⁴

Size of the nucleus

Size of the nucleus depends on the number of nucleons present in it. The statistical radius of a nucleus is given by the expression. R = R₀A^(1/3) Where, R₀ = 1 × 10⁻¹⁵ m. A = mass number of the nucleus

Mass defect

Mass of the nucleus is less than the total mass of the nucleons. The difference of the total mass of the nucleus and mass the nucleus is called mass defect. For example atomic number of an atom is Z and its mass number is A (zX^A). Its mass defect, Δm = Zmp + (A-Z) mn – m (ZX^A)

Binding Energy

The amount of energy needed to separate the nucleons of a nucleus by large distance is called the binding energy (i.e. to split the nucleus). Numerically it is the energy equivalent to mass defect. B.E. = ΔmC² If mass is measured in amu then B.E. = Δm × 931.5M eV As 1 amu = 931.5 M eV.  This binding energy curve has the following features:

i. With the exception of the lighter nuclei, the average binding energy per nucleon is around 8MeV. This shows that the nuclear force saturates.

ii. The curve has a maximum around A = 60. This means that nuclei with mass numbers around 60have the greatest stability.

iii. The decline in the curve at high mass numbers tells us that energy can be released by breaking a single heavy nucleus into two smaller fragments. The mass number of each of the two smaller fragments will, of course, be greater than 60. Such a process is called nuclear fission.

iv. The steep decline in he curve at low mass numbers indicates that energy will also be released if two very light nuclides combine to form a single nucleus. The mass number of this composite nucleus will, however, be less than 60. This process is called nuclear fusion.

V. Certain "kinks' in the binding energy curve on the side of low mass numbers signify the exceptionally higher binding energy per nucleon of the nuclide than its neighbours.

Nuclear Stability (Nuclear force)

In nucleus protons are together in infinitesimal volume, and hence they are acted upon by a large electrostatic repulsive force. However nuclei are stable because of the presence of nuclear force. Nuclear force comes into play when distance between two particles reduces to the order of 10⁻¹⁴ m. Nuclear force is attractive force irrespective of the nature of charges on the particles. For the given range nuclear force is 50 to 60 times greater than electrostatic force. The nucleus having more binding energy per nucleon is more stable.

Radioactivity

When electrostatic repulsive force in the nucleus dominates the nuclear force, then it disintegrates. Disintegration of nucleus is known as radioactivity.

Laws of radioactivity

At any time rate of disintegration of a sample is directly proportional to number of active nuclei present in the sample at that time. i.e. dN/dt = -λN Here λ is a constant (called decay constant) and N is the instantaneous number of active nuclei. If at t = 0 number of active nuclei be N₀ and at any time it is Nt then Nt = N₀e^(-λt)

This expression gives the relation between instantaneous number of active nuclei and initial number of active nuclei. The quantity (-dN/dt) gives the number of decays per unit time and is known as activity of the sample.

A(t) = λNt = λN₀e^(-λt) ∴ At = A₀e^(-λt)

Unit of Activity

SI unit of activity is Becquerel (Bq) 1 Becquerel = 1 disintegration per second. Popular unit of activity is curie (Ci) 1 Curie = 3.7 × 10¹⁰ disintegration per second.

Half Life

The time interval in which number of active nuclei reduces to half of its initial value is called half-life. Half life is denoted by T₁/₂ and is given by T₁/₂ = 0.693/λ

Average Life

Average life of a radioactive element is given by τ = 1/λ.

Formulae And Concepts At A Glance

1. Wavelength associated with particles of momentum P is given by λ = h/p = h/(mv)
2. For an electron accelerated through a pd v; λ = h/√(2eVme)
3. Angular momentum of an electron revolving in an orbit is mentioned L = mvr = nh/(2π)
4. The minimum energy needed to eject an electron from the surface of the metal is known as work function of the metal.
5. Maximum K.E. of photo electron, T = E – W = h (v-v₀).
6. Mass defect Δm = Zmp + (A-Z)mn – m(ZX^A)
7. Binding energy = ΔmC² 1 amu = 931.5 MeV
8. Nt = N₀e^(-λt)
9. T₁/₂ = 0.693/λ

Solved Examples

Problem-1: A spectral line results from the transition n =2 to n =1, in the atoms/species given below which one of these will produce the shortest wavelength emission? (A) Hydrogen atom (B) Singly ionised Helium (C) Doubly ionized Lithium (D) Deuterium atoms

Solution: According to Bohr theory 1/λ = RZ² [(1/n₁²) - (1/n₂²)] Thus λ ∝ 1/Z² More the atomic number, smaller is the wavelength obtained in the transition of electron (for identical transition). Thus the answer is (C).

Problem-2: When an electron jumps from an orbit with n = 1 to n = 2, the change in orbital angular momentum is (A) h/(2π) (B) h/(4π) (C) 3h/(4π) (D) Zero

Solution: According to Bohr postulates for hydrogen like atoms, electron can orbit in those orbits in which it's orbital angular momentum is integral multiple of h/2π.

Thus change in orbital angular momentum = (2h)/(2π) - (1h)/(2π) = h/(2π)

Thus the answer is (A)

Assignment

Q. A hydrogen like atom has a μ meson of mass 200 times that of an electron, bound to the proton. The radius of the first Bohr orbit of the muonic atom will be

(A) Equal to that of Hydrogen

(B) 400 times that of hydrogen

(C) 200 times that of hydrogen

(D) 1/200 times that of hydrogen

Q. In a hydrogen atom, the electron moves in an orbit of radius 0.5 A° making 10²⁶ revolutions per second. The magnetic moment associated with the orbital motion of the electron is (in Amp – m²)

(A) 4π × 10⁻¹⁴

(B) 2π × 10⁻¹⁴

(C) 8π × 10⁻¹⁴

(D) None of the above

Q. The wavelength of spectral line for an electronic transition is inversely related to

(A) The number of electrons undergoing transition

(B) The nuclear charge of the atom

(C) The difference in the energy of the energy levels involved in the transition

(D) The velocity of the electron undergoing the transition.

Q. The Bohr radius of the fifth electron of phosphorus atom (atomic number = 15) acting as a dopant in silicon (relative dielectric constant 12) is ……… A°

(A) 101.76

(B) 57.24

(C) 6.7 A°

(D) 0.53

Q. In the Bohr model of the hydrogen atom, the ratio of kinetic energy to the total energy of the electron in a quantum state n is …………………

(A) +1

(B) -1/2

(C) -1

(D) +2

Q. Which one of the series of hydrogen spectrum is in the visible region

(A) Lyman series

(B) Balmer series

(C) Paschen series

(D) Bracket series

Q. If we consider electrons and photons of same wavelength, then they will have same

(A) Energy

(B) Velocity

(C) Momentum

(D) Angular Momentum

Q. An electron of mass m, when accelerated through a potential v, has deBroglie wavelength λ. The deBroglie wavelength associated with a photon of mass M accelerated through the same potential difference will be

(A) λ√(m/M)

(B) λ√(M/m)

(C) λ(m/M)

(D) λ√(m/M)

Q. The energy E and the momentum P of photon is given by E = hν and p = h/λ, the velocity of photon will be

(A) E/p

(B) Ep

(C) (E/p)²

(D) (E/p)^(1/2)

Q. The electrical conductivity of a semi conductor increases when electromagnetic radiation of wavelength shorter than 2480 nm is incident on it. The band gap (in eV) for the semiconductor is.

(A) 0.9

(B) 0.7

(C) 0.5

(D) 1.1

Q. Which of the following statement is correct?

(A) the current in photocell increases with increasing frequency

(B) the photo current increases with intensity of light

(C) the photo current is proportional to the applied voltage

(D) the stopping potential increases with increase of incident – light.

Q. The maximum kinetic energy (Kmax) of photoelectrons emitted in a photoelectric cell is measured using lights of various frequencies v. The slope of the graph is equal to

(A) change on an electron

(B) work function of emitter

(C) velocity of photon

(D) plank's constant

Q. In photoelectric effect, the slope of straight line graph between stopping potential (v₀) and frequency of incident light (ν) gives.

(A) change on electron

(B) work function of emitter

(C) Planck's constant

(D) ratio of Planck's constant to charge on electron

Q. The correct sequence of the increasing wavelength of the given radiation sources is

(A) Radioactive source, X-ray tube, crystal oscillator, sodium vapour lamp

(B) Radioactive source, X-ray tube, sodium vapour lamp crystal oscillator

(C) X-ray tube, radioactive source, crystal oscillator, sodium vapour lamp

(D) X-ray tube, crystal oscillator, radioactive source, sodium vapour lamp

Q. Mosley's law is concerned with

(A) Continuous X-ray

(B) Characteristic X-ray

(C) laser light

(D) Radioactivity

Answers

1. D

2. A

3. C

4. C

5. C

6. B

7. C

8. B

9. A

10. C

11. B

12. D

13. D

14. B

15. B